
【题目】已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.
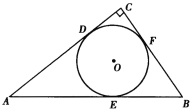
(1)若AC=12cm,BC=9cm,求⊙O的半径r;
(2)若AC=b,BC=a,AB=c,求⊙O的半径r.
【答案】(1)r=3cm. (2) r=![]() (a+b-c).
(a+b-c).
【解析】
首先设AC、AB、BC与⊙O的切点分别为D、E、F;易证得四边形OFCD是正方形;那么根据切线长定理可得: CD=CF=![]() (AC+BC-AB),由此可求出r的长.
(AC+BC-AB),由此可求出r的长.
(1)如图,连接OD,OF;
在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm;
根据勾股定理AB=![]() =15cm;
=15cm;
四边形OFCD中,OD=OF,∠ODC=∠OFC=∠C=90°;
则四边形OFCD是正方形;由切线长定理,得:AD=AE,CD=CF,BE=BF;
则CD=CF=![]() (AC+BC-AB);
(AC+BC-AB);
即:r=![]() (12+9-15)=3cm.
(12+9-15)=3cm.
(2)当AC=b,BC=a,AB=c,由以上可得: CD=CF=![]() (AC+BC-AB);
(AC+BC-AB);
即:r=![]() (a+b-c).则⊙O的半径r为:
(a+b-c).则⊙O的半径r为:![]() (a+b-c).
(a+b-c).


科目:初中数学 来源: 题型:
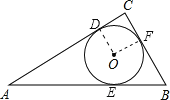
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形ABCD在直线上绕其右下角的顶点B向右旋转90°至矩形A′BC′D′的位置,再绕右下角的顶点C′继续向右旋转90°至矩形A′′B′C′D′′的位置,……,以此类推,这样连续旋转2 019次后,顶点A在整个旋转过程中所经过的路线之和是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
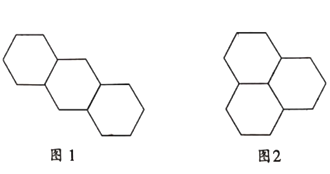
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-(2k-1)x+k2,其中k是常数.
(1)若该抛物线与x轴有交点,求k的取值范围;
(2)若此抛物线与x轴其中一个交点的坐标为(-1,0),试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;②做n次随机试验,事件A发生m次,则事件A发生的概率一定等于![]() ;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
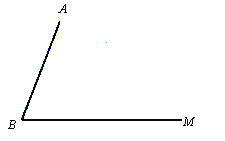
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
(1)求直线![]() 的表达式;
的表达式;
(2)过点A做平行于x轴的直线l,l与抛物线![]() (a>0)交于B,C两点。若BC≥4,求a的取值范围;
(a>0)交于B,C两点。若BC≥4,求a的取值范围;
(3)设直线![]() 与抛物线
与抛物线![]() 交于D,E两点,当3
交于D,E两点,当3![]() ≤DE≤5
≤DE≤5![]() 时,结合函数的图象,直接写出m的取值范围是____________________。
时,结合函数的图象,直接写出m的取值范围是____________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com