
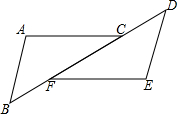
 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
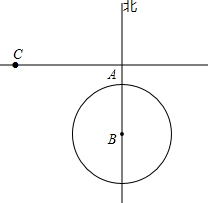 如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).
如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).查看答案和解析>>
科目:初中数学 来源: 题型:
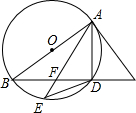 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
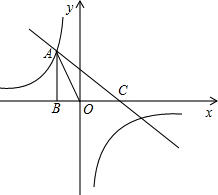 如图,已知反比例函数y1=
如图,已知反比例函数y1=| k |
| x |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AB |
| GF |
| 6 |
| 5 |
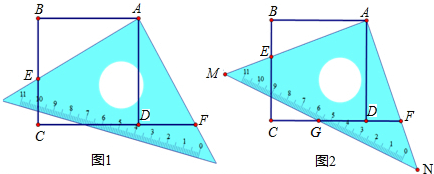
查看答案和解析>>
科目:初中数学 来源: 题型:
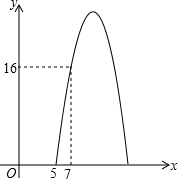 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 5 |
| PE |
| AP |
| 1 |
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com