
 如图,AD丄BC于点D,EF丄BC于点F,且∠E=∠1,请问:∠BAD和∠CAD相等吗?并说明理由.
如图,AD丄BC于点D,EF丄BC于点F,且∠E=∠1,请问:∠BAD和∠CAD相等吗?并说明理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )| A. | 过一点有无数条直线 | |
| B. | 两点之间线段的长度,叫做这两点之间的距离 | |
| C. | 两点确定一条直线 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
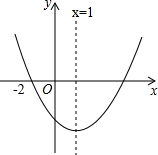 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com