
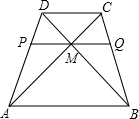
 过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.
过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| PD |
| DA |
| PD |
| PD+AP |
| 1 |
| 3 |
| 1 |
| 3 |
| AP |
| AD |
| 2 |
| 3 |
| 2 |
| 3 |
| PM |
| CD |
| AP |
| AD |
| 2 |
| 3 |
| PM |
| AB |
| 1 |
| 3 |
| CD |
| AB |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
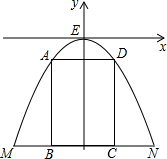 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.查看答案和解析>>
科目:初中数学 来源: 题型:
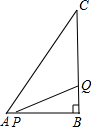 如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?查看答案和解析>>
科目:初中数学 来源: 题型:
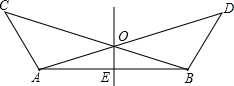 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
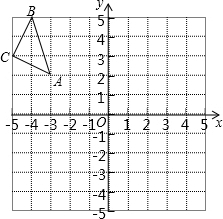 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com