
【题目】![]() 尺规作图1:
尺规作图1:
已知:如图,线段AB和直线且点B在直线上
求作:点C,使点C在直线上并且使![]() 为等腰三角形.
为等腰三角形.
作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C.
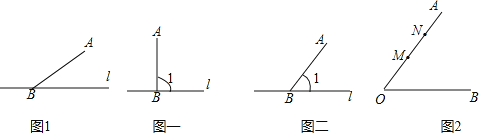
![]() 特例思考:
特例思考:
如图一,当![]() 时,符合
时,符合![]() 中条件的点C有______个;如图二,当
中条件的点C有______个;如图二,当![]() 时,符合
时,符合![]() 中条件的点C有______个
中条件的点C有______个![]()
![]() 拓展应用:
拓展应用:
如图,![]() ,点M,N在射线OA上,
,点M,N在射线OA上,![]() ,
,![]() ,点P是射线OB上的点
,点P是射线OB上的点![]() 若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值.
若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值.
【答案】(1) 见解析;(2) 2,2 ;(3)0或![]() 或
或![]() .
.
【解析】
![]() 根据等腰三角形的定义,用分类讨论的思想解决问题即可;
根据等腰三角形的定义,用分类讨论的思想解决问题即可;
![]() 通过画图分析可得,当
通过画图分析可得,当![]() 时,符合
时,符合![]() 中条件的点C有2个,当
中条件的点C有2个,当![]() 时,符合
时,符合![]() 中条件的点C有2个;
中条件的点C有2个;
![]() 分三种情形讨论求解即可.
分三种情形讨论求解即可.
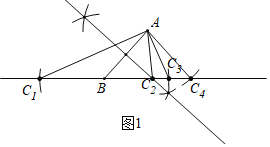
解:![]() 如图1中,点
如图1中,点![]() ,
,![]() ,
,![]() ,
,![]() 即为所求.
即为所求.
![]() 如图一,当
如图一,当![]() 时,符合
时,符合![]() 中条件的点C有2个;如图二,当
中条件的点C有2个;如图二,当![]() 时,符合
时,符合![]() 中条件的点C有2个,
中条件的点C有2个,
当∠1=90°或∠1=60°时,符合条件的点C都是在点B左右各一个,当∠1=60°时,符合条件的点C如图所示:
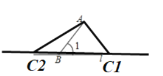
故答案为2,2.
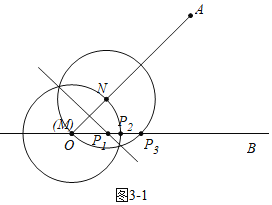
![]() 如图
如图![]() 中,当
中,当![]() 时,当
时,当![]() 时,有点
时,有点![]() ,当
,当![]() 时,有点
时,有点![]() ,当
,当![]() 时,有点
时,有点![]() ,此时有3个P点.
,此时有3个P点.
![]() 如图
如图![]() 中,当
中,当![]() 与OB相切于点
与OB相切于点![]() 时,
时,
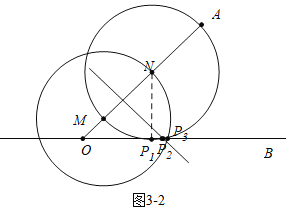
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,此时有3个P点.
,此时有3个P点.
![]() 如图
如图![]() 中,当
中,当![]() 经过点O时,此时只有2个P点,
经过点O时,此时只有2个P点,
如图![]() 中,
中,![]() 与OB相交时,此时有3个P点,
与OB相交时,此时有3个P点,
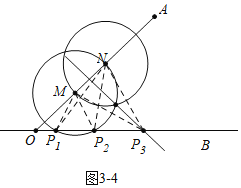
如图![]() 中,当
中,当![]() 与OB相切时,只有2个P点.
与OB相切时,只有2个P点.

此时![]() ,
,
综上所述,当![]() 时,有3个P点.
时,有3个P点.
![]() 满足条件的x的值为0或
满足条件的x的值为0或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式,并指出比例系数;
(2)若要5天完成总任务,则每天产量应达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
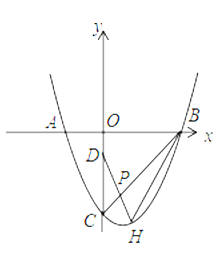
【题目】如图,在平面直角坐标系中,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() ,点
,点![]() 为线段
为线段![]() 上一动点,延长
上一动点,延长![]() 交抛物线于点
交抛物线于点![]() ,连结
,连结![]() .
.
①当四边形![]() 面积为9,求点
面积为9,求点![]() 的坐标;
的坐标;
②设![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
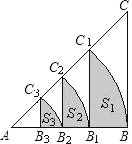
【题目】如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 | 成活数 | 成活率 | 移植棵数 | 成活数 | 成活率 |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
下面有四个推断:
①当移植的树数是1500时,表格记录成活数是1335,所以这种树苗成活的概率是![]() ;
;
②随着移植棵数的增加,树苗成活的频率总在![]() 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是
附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是![]() ;
;
③若小张移植10000棵这种树苗,则可能成活9000棵;
④若小张移植20000棵这种树苗,则一定成活18000棵.
其中合理的是![]()
![]()
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
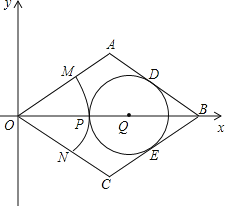
【题目】如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边在直线y=![]() x上,AB边在直线y=-
x上,AB边在直线y=-![]() x+2上.
x+2上.
(1)直接写出:线段OA等于多少,∠AOC等于多少度;
(2)在对角线OB上有一动点P,以O为圆心,OP为半径画弧MN,分别交菱形的边OA、OC于点M、N,作⊙Q与边AB、BC、弧MN都相切,⊙Q分别与边AB、BC相切于点D、E,设⊙Q的半径为r,OP的长为y,求y与r之间的函数关系式,并写出自变量r的取值范围;
(3)若以O为圆心、OA长为半径作扇形OAC,请问在菱形OABC中,在除去扇形OAC后的剩余部分内,是否可以截下一个圆,使得它与扇形OAC刚好围成一个圆锥,若可以,求出这个圆的半径,若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
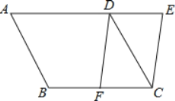
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .在同一平面直线坐标系中
.在同一平面直线坐标系中
(![]() )若函数
)若函数![]() 的图象过点
的图象过点![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,求
,求![]() ,
, ![]() 的值.
的值.
(![]() )若函数
)若函数![]() 的图象经过
的图象经过![]() 的顶点.
的顶点.
①求证: ![]() .
.
②当![]() 时,比较
时,比较![]() ,
, ![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com