
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )| A、2 | B、3 | C、4 | D、5 |
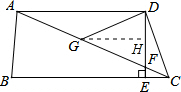 解:∵AD∥BC,DE⊥BC,
解:∵AD∥BC,DE⊥BC,| CD2-EC2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
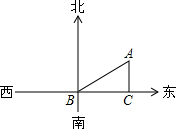 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)
一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)查看答案和解析>>
科目:初中数学 来源: 题型:
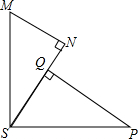 如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )
如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )| A、∠A=∠QSP |
| B、∠MSN=∠P |
| C、MS=SP |
| D、MN=QN |
查看答案和解析>>
科目:初中数学 来源: 题型:
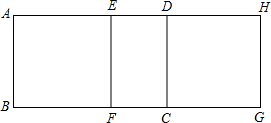 如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:
如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com