
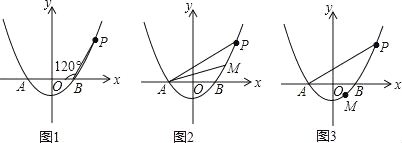
【题目】(2016湖南省邵阳市第26题)已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
【答案】(1)、y=![]() x2﹣
x2﹣![]() ;(2)、①、(3,
;(2)、①、(3,![]() );②、(
);②、(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
【解析】
试题分析:(1)、先求出A、B两点坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;(2)、①过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、M的坐标,然后代入△APM的面积公式![]() DMAC,根据题意列出方程求出m的值;②根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
DMAC,根据题意列出方程求出m的值;②根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
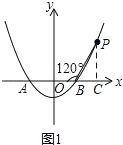
试题解析:(1)、如图1,令y=0代入y=ax2﹣4a, ∴0=ax2﹣4a, ∵a>0, ∴x2﹣4=0,
∴x=±2, ∴A(﹣2,0),B(2,0), ∴AB=4, 过点P作PC⊥x轴于点C, ∴∠PBC=180°﹣∠PBA=60°,
∵PB=AB=4, ∴cos∠PBC=![]() , ∴BC=2, 由勾股定理可求得:PC=2
, ∴BC=2, 由勾股定理可求得:PC=2![]() , ∵OC=OC+BC=4,
, ∵OC=OC+BC=4,
∴P(4,2![]() ), 把P(4,2
), 把P(4,2![]() )代入y=ax2﹣4a, ∴2
)代入y=ax2﹣4a, ∴2![]() =16a﹣4a, ∴a=
=16a﹣4a, ∴a=![]() ,
,
∴抛物线解析式为;y=![]() x2﹣
x2﹣![]() ;
;
(2)∵点M在抛物线上, ∴n=![]() m2﹣
m2﹣![]() , ∴M的坐标为(m,
, ∴M的坐标为(m,![]() m2﹣
m2﹣![]() ),
),
①当点M在曲线PB之间(含端点)移动时, ∴2≤m≤4,
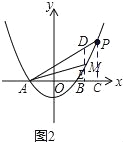
如图2,过点M作ME⊥x轴于点E,交AP于点D, 设直线AP的解析式为y=kx+b,
把A(﹣2,0)与P(4,2![]() )代入y=kx+b,得:
)代入y=kx+b,得:![]() , 解得
, 解得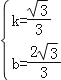
∴直线AP的解析式为:y=![]() x+
x+![]() , 令x=m代入y=
, 令x=m代入y=![]() x+
x+![]() , ∴y=
, ∴y=![]() m+
m+![]() ,
,
∴D的坐标为(m,![]() m+
m+![]() ), ∴DM=(
), ∴DM=(![]() m+
m+![]() )﹣(
)﹣(![]() m2﹣
m2﹣![]() )=﹣
)=﹣![]() m2+
m2+![]() m+
m+![]()
![]() ,
,
∴S△APM=![]() DMAE+
DMAE+![]() DMCE=
DMCE=![]() DM(AE+CE)=
DM(AE+CE)=![]() DMAC=﹣
DMAC=﹣m2+
![]() m+4
m+4![]()
当S△APM=![]()
![]() 时,∴
时,∴![]()
![]() =﹣
=﹣![]() m2+
m2+![]() m+4
m+4![]() , ∴解得m=3或m=﹣1, ∵2≤m≤4,
, ∴解得m=3或m=﹣1, ∵2≤m≤4,
∴m=3, 此时,M的坐标为(3,![]() );
);
②当点M在曲线BA之间(含端点)移动时, ∴﹣2≤m≤2,n<0,
当﹣2≤m≤0时, ∴|m|+|n|=﹣m﹣n=﹣![]() m2﹣m+
m2﹣m+![]() =﹣
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
当m=﹣![]() 时, ∴|m|+|n|可取得最大值,最大值为
时, ∴|m|+|n|可取得最大值,最大值为![]()
![]() ,
,
此时,M的坐标为(﹣![]() ,﹣
,﹣![]() ), 当0<m≤2时,
), 当0<m≤2时,
∴|m|+|n|=m﹣n=﹣![]() m2+m+
m2+m+![]() =﹣
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
当m=![]() 时, ∴|m|+|n|可取得最大值,最大值为
时, ∴|m|+|n|可取得最大值,最大值为![]()
![]() , 此时,M的坐标为(
, 此时,M的坐标为(![]() ,﹣
,﹣![]() ),
),
综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
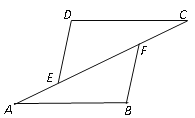
【题目】如图6,已知A、E、F、C四点共线,BF=DE,AB=CD.
(1)请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使△DEC ≌△BFA,并给出证明.你添加的条件是:_______________;
(2)在(1)的基础上,求证:DE∥BF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某市五月份第二周连续七天的空气质量指数分别为:111、96、47、68、70、77、105,则这七天空气质量指数的平均数是( )
A.71.8
B.77
C.82
D.95.7
查看答案和解析>>
科目:初中数学 来源: 题型:
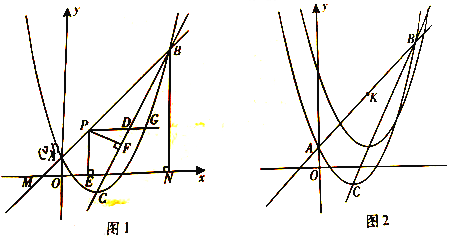
【题目】(2016重庆市第26题)如图1,二次函数![]() 的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD//x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数![]() 沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市元宵节灯展参观人数约为470000,将这个数用科学记数法表示为( )
A. 4.7×106 B. 4.7×105 C. 0.47×106 D. 47×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B和点C分别为∠MAN两边上的点,AB=AC.

(1)按下列语句画出图形:(要求不写作法,保留作图痕迹)
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E;
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用计算器计算各式:6×7= ,66×67= ,666×667= ,6 666×6 667= .
(1)根据以上结果,你发现了什么规律?
(2)依照你发现的规律,不用计算器,你能直接写出666 666×666 667的结果吗?请你试一试.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com