Question

3．如图、直角梯形ABCD中、AB∥CD、∠D=90°、DE⊥CB于E、连接AE，FE垂直AE交CD于F．
（1）求证：△AED∽△FEC；
（2）求证：AB=DF；
（3）若AD=CD．$\frac{{S}_{△AEB}}{{S}_{△DEF}}$=2，则$\frac{AB}{CD}$=$\frac{-1+\sqrt{5}}{2}$．

Answer 1

分析 （1）根据条件可以得出∠EFC=∠EAD，∠CEF=∠AED，进而可以证明△AED∽△FEC．
（2）根据条件可以证明A、D、F、B、A四点共圆，由∠BEA=∠FED，推出结论．
（3）设AB=a，CD=b，通过辅助线，利用方程的思想，解决问题．

解答 解：（1）∵DE⊥BC，EF⊥AE，
∴∠BED=∠CED=90°，
∵∠2+∠3=90°，∠2+∠CEF=90°，
∴∠CEF=∠3，
∵∠AEF=∠ADF=90°
∴∠6+∠4=180°，∵∠5+∠6=180°，
∴∠5=∠4，
∴△ADE∽△FEC．
（2）∵∠1+∠3=90°，∠2+∠3=90°，
∴∠1=∠2，
∵AB∥CD，∠ADC=90°，
∴∠BAD+∠ADC=180°，∴∠BAD=90°，
∵∠BED+∠BAD=180°，
∴四边形ABCD四点共圆，
∵∠AEF+∠ADF=180°，
∴四边形AEFD四点共圆，
∴A、B、E、F、D五点共圆，
∵∠1=∠2，
∴AB=DF．
（3）作CN⊥AB交AB的延长线于N，过点E作EG⊥AN垂足为G交CD于H，延长DE交CN于M．
∵$\frac{{S}_{△ABE}}{{S}_{△EDF}}$=$\frac{\frac{1}{2}•AB•EG}{\frac{1}{2}•DF•EH}$=2，AB=FD，
∴EG=2EH，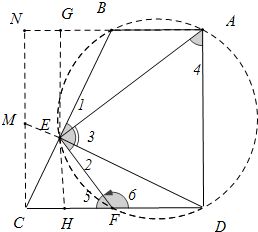
∵GB∥CH，
∴△EGB∽△EHC，
∴$\frac{EG}{EH}=\frac{EB}{EC}=2$，设EC=a，AB=x，CD=y，则EB=2a，
∵∠NCD=∠ADC=∠DAN=90°，
∴四边形ADCN是矩形，
∵AD=DC
∴四边形ADCN是正方形，
∴AN=CN=CD=y，NB=y-x，
∵∠NCB+∠CMD=90°，∠CMD+∠MDC=90°
∴∠NCB=∠MDC，∵CN=CD，
∴△CNB≌△DCM，
∴CM=BN=y-x，DM=BC=3a，
∵∠MCD=∠MEC，∠CME=∠CMD，
∴△MCE∽△MDC，
∴$\frac{MC}{MD}=\frac{CE}{CD}$，
∴$\frac{y-x}{3a}=\frac{a}{y}$，
∴y²-xy=3a²     ①
∵CM²+CD²=MD²，
∴（y-x）²+y²=9a²    ②
由①②消去a得x²+xy-y²=0
∴x=$\frac{-1+\sqrt{5}}{2}$y，（或x=$\frac{-1-\sqrt{5}}{2}$y舍弃）
∴$\frac{x}{y}=\frac{-1+\sqrt{5}}{2}$，
∴$\frac{AB}{CD}=\frac{-1+\sqrt{5}}{2}$．

点评 本题考查了直角梯形的性质、正方形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质、以及四点共圆的判定，综合性比较强，用方程的思想是解决第三个问题的关键．