
| A. | 1,1,$\sqrt{2}$ | B. | 12,16,20 | C. | 1,$\frac{4}{3}$,$\frac{5}{3}$ | D. | 1,2,2 |
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:选择题
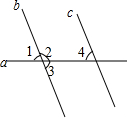 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )| A. | ∠2=115° | B. | ∠3=65° | C. | ∠4=65° | D. | ∠4=115° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
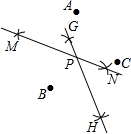 如图所示的是A、B、C、D三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B、C两点为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于G、H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
如图所示的是A、B、C、D三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B、C两点为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于G、H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )| A. | 100° | B. | 120° | C. | 132° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
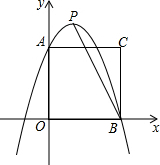 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com