
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B,C两点,与y轴交于点D(0,3).
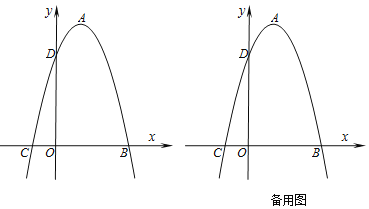
(1)求抛物线的表达式以及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,使得DP+CP最小,如果存在,求出点P的坐标;如果不存在,请说明理由.
(3)点Q是线段BD上方抛物线上的一个动点.过点Q作x轴的垂线,交线段BD于点E,再过点Q作QF∥x轴交抛物线于点F,连结EF,请问是否存在点Q使△QEF为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;B的坐标是(3,0);(2)存在,P的坐标是(1,2);(3)存在,点Q的坐标为(2,3)或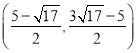
【解析】
(1)根据顶点坐标,则设顶点式,代入点C的坐标即可求出抛物线的解析式;令y=0,求得x的值,从而得到点B的坐标;
(2)根据轴对称的最短路径问题,连接DB交对称轴于P,此时PD+PB=PD+PC的值最小,先求E'F的解析式,它与对称轴的交点就是所求的点G;
(3)设Q(n,﹣n2+2n+3),则E(n,﹣n+3),F(﹣n+2,﹣n2+2n+3),所以可以用![]() 的代数式表示QE和QF的长,由题意得QE=QF即﹣n2+3n=|2n﹣2|,即可求得符合题意的
的代数式表示QE和QF的长,由题意得QE=QF即﹣n2+3n=|2n﹣2|,即可求得符合题意的![]() 的值,从而求得点Q的坐标.
的值,从而求得点Q的坐标.
(1)∵抛物线的顶点A的坐标为(1,4),
∴设抛物线的表达式为:y=a(x﹣1)2+4,
把(0,3)代入得:3=a(0﹣1)2+4,a=﹣1,
∴抛物线的表达式为:y=﹣(x﹣1)2+4=﹣x2+2x+3;
令y=0,﹣(x﹣1)2+4=0,解得x1=3,x2=﹣1,
∴B的坐标是(3,0),C的坐标是(﹣1,0);
(2)存在,
如图1,因为B,C关于对称轴对称,连接BD交对称轴于P,此时DP+CP的值最小,
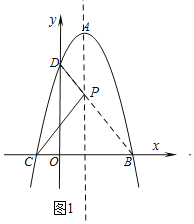
∵D(0,3),B(3,0),易得BD的解析式为:y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴P的坐标是(1,2);
(3)如图2,存在点Q,使△QEF为等腰直角三角形,

设Q(n,﹣n2+2n+3),则E(n,﹣n+3),F(﹣n+2,﹣n2+2n+3),
∴QE=(﹣n2+2n+3)﹣(﹣n+3)=﹣n2+3n,QF=|2n﹣2|,
∵QE⊥x轴、QF∥x轴,
∴∠EQF=90°,
∴当QE=QF时,△QEF为等腰直角三角形,即:﹣n2+3n=|2n﹣2|,
①﹣n2+3n=2n﹣2,即:![]() ,即:
,即:![]()
解得:n1=﹣1(不合题意,舍去),n2=2,
则Q(2,3);
②﹣n2+3n=﹣2n+2,即:![]() ,
,
解得:n1=![]() >3(不合题意,舍去),n2=
>3(不合题意,舍去),n2=![]() ,
,
则Q(![]() ,
,![]() ).
).
综上,点Q的坐标为(2,3)或(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(﹣4,0)、B(﹣l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ACD的面积为量求出S与m的函数关系式,并确定m为何值时S有最大值,最大值是多少?
(3)若点P是抛物线对称轴上一点,是否存在点P使得∠APC=90°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
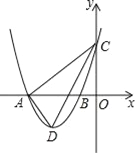
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12![]() 时,OA的长为____.
时,OA的长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全校的科技制作大赛中,王浩同学用木板制作了一个带有卡槽的三角形手机架.如图所示,卡槽的宽度DF与内三角形ABC的AB边长相等.已知AC=20cm,BC=18cm,∠ACB=50°,一块手机的最长边为17cm,王浩同学能否将此手机立放入卡槽内?请说明你的理由(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
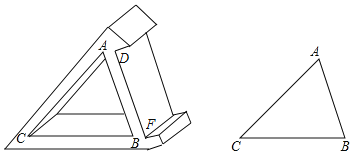
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
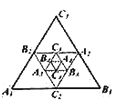
【题目】如图,小红作出了边长为1的第1个等边![]() ,算出了等边
,算出了等边![]() 的面积,然后分别取
的面积,然后分别取![]() 三边的中点
三边的中点![]() 、
、![]() 、
、![]() ,作出了第2个等边
,作出了第2个等边![]() ,算出了等边
,算出了等边![]() 的面积,用同样的方法,作出了第3个等边
的面积,用同样的方法,作出了第3个等边![]() ,算出了等边
,算出了等边![]() 的面积……,由此可得,第
的面积……,由此可得,第![]() 个等边
个等边![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com