
分析 (1)如图①中作DM⊥AC于M,DN⊥CB于N,连接AD,因为AD=$\sqrt{2}$AB,欲证明CD=$\sqrt{2}$AB,只要证明AD=CD即可,可以通过证明四边形MCND是矩形,得DN=CM=BC=AM,又DM⊥AC由此可以得到证明.
(2))如图②中作DM⊥CA于M,由△MAD≌△CBA得AM=BC=1,DM=AC=2BC=2,在RT△CDM中利用勾股定理即可.
(3)如图③中作DN⊥AC于N,DM⊥CB于M,只要证明△ADN≌△BDM,四边形NCMD是正方形,求出正方形边长即可解决.
解答 (1)证明:如图①中,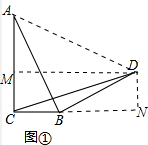 作DM⊥AC于M,DN⊥CB于N,连接AD.
作DM⊥AC于M,DN⊥CB于N,连接AD.
∵∠ABD=90°,∠ACB=∠DNC=90°,
∴∠ABC+∠DBN=90°,∠CAB+∠ABC=90°,
∴∠CAB=∠DBN,
在△ACB和△BND中,
$\left\{\begin{array}{l}{∠ACB=∠DNB}\\{∠CAB=∠DBN}\\{AB=DB}\end{array}\right.$,
∴△ACB≌△BND,
∴BC=DN,
∵∠DMC=∠MCN=∠DNC=90°,
∴四边形MCND是矩形,
∴MC=DN=BC,
∵AC=2BC,
∴AM=CM=BC,∵DM⊥AC,
∴DA=DC,
∵∠ABD=90°,AB=DB,
∴AD=$\sqrt{2}$AB,
∴CD=$\sqrt{2}$AB.
(2)如图②中,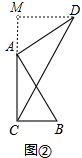 作DM⊥CA于M,
作DM⊥CA于M,
∵∠DAB=∠DMA=∠ACB=90°,
∴∠MAD+∠CAB=90°,∠CAB+∠ABC=90°,
∴∠MAD=∠ABC,
在△MAD和△CBA中,
$\left\{\begin{array}{l}{∠M=∠ACB}\\{∠MAD=∠ABC}\\{AD=AB}\end{array}\right.$,
∴△MAD≌△CBA,
∴AM=BC=1,DM=AC=2BC=2,
在RT△CMD中,∵CM=AC+AM=3,MD=1,
∴CD=$\sqrt{C{M}^{2}+M{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
(3)如图③中,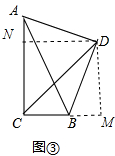 作DN⊥AC于N,DM⊥CB于M.
作DN⊥AC于N,DM⊥CB于M.
在RT△ABC中,∵AC=2BC,AB=2$\sqrt{5}$,设BC=a,则AC=2a,
∴a2+4a2=20
∵a>0,
∴a=2,
∴BC=2,AC=4,
∵∠NCM=∠DNC=∠DMC=90°,
∴四边形NCMD是矩形,
∴∠MDN=∠ADB=90°,
∴∠ADN=∠BDM,
在△ADN和△BDM中,
$\left\{\begin{array}{l}{∠AND=∠DMB}\\{∠ADN=∠BDM}\\{DA=DB}\end{array}\right.$,
∴△ADN≌△BDM,
∴DM=DN,
∴四边形NCMD是正方形,
∴CN=CM=DM=DN,设CN=CM=DM=DN=x,
∴AC-AN=BC+BM,
∴4-x=2+x,
∴x=1,
∴CM=DM=3,
在RT△CDM中,CD=$\sqrt{C{M}^{2}+D{M}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
点评 本题考查全等三角形的判定和性质、勾股定理、矩形和正方形的判定和性质,添加辅助线构造全等三角形是解决问题的关键,属于参考常考题型.


科目:初中数学 来源: 题型:选择题
 在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )
在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
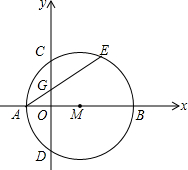 如图,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4.
如图,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 西兰花 | 胡萝卜 |
| 批发价(元/kg) | 2.8 | 1.6 |
| 零售价(元/kg) | 3.8 | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com