
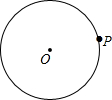
 链球运动员在投掷链球时,链球按顺时针作圆周运动,如图,当运动员即将放手时,链球在⊙O的点P处.
链球运动员在投掷链球时,链球按顺时针作圆周运动,如图,当运动员即将放手时,链球在⊙O的点P处.分析 (1)连接OP,过点P作OP的垂线PA,则PA为链球飞出的方向;
(2)根据切线的性质得∠APO=90°,然后在Rt△OPA中利用勾股定理计算OA即可.
解答 解:(1)如图,PA方向为链球飞出的方向;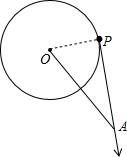
(2)如图,连接OP,OP=1.2m,PA=32m,
∵PA为⊙O的切线,
∴OP⊥PA,
∴∠APO=90°,
在Rt△OPA中,OA=$\sqrt{O{P}^{2}+P{A}^{2}}$=$\sqrt{1.{2}^{2}+3{2}^{2}}$≈32.02(m).
答:此时链球离点O的距离约为32.02m.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题
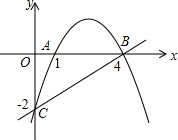 如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).
如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.
如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com