练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．用一副三角板共能拼出11个小于平角的角，度数分别为15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°．

    分析 一副三角板有30°，45°，60°，90°，所以利用角之间的和与差进而可得一些角度的大小．

    解答 解：因为三角板有30°，45°，60°，90°，可利用角度的和与差作出角度，所以作出的角度应为15°的倍数，且小于180°，
    这些角的度数分别是：15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°，
    共11个，
    故答案为11；15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°．

    点评 本题考查了角的计算，难度一般，关键是知道一副三角板中的度数分别是多少，能够利用三角板作出一些简单的角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

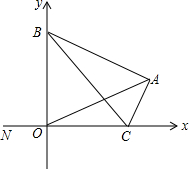    14．如图所示，在平面直角坐标系xOy中，△ABC的顶点B是y轴正半轴上一个定点，D是BO的中点．点C在x轴上，A在第一象限，且满足AB=AO，N是x轴负半轴上一点，∠BCN=∠BAO=α．
    （1）当点C在x轴正半轴上移动时，求∠BCA；（结果用含α的式子表示）
    （2）当某一时刻A（20，17）时，求OC+BC的值；
    （3）当点C沿x轴负方向移动且与点O重合时，α=90°，此时 以AO为斜边在坐标平面内作一个Rt△AOE（E不与D重合），则∠AED的度数的所有可能值有45°或135°．（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，已知点C在线段AB上，且AM=$\frac{1}{3}$AC．BN=$\frac{1}{3}$BC

    （1）若AC=12，CB=6，求线段MN的长；
    （2）若点C为线段AB上任意一点，且满足AC+BC=a，请直接写出线段MN的长；
    （3）如图2若点C为线段AB延长线上任意一点，且满足AC-CB=b，求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：A（4，0），点B是y轴上一动点，点C在x轴上，AC=5．
    （1）直接写出点C的坐标；
    （2）若S△ABC=10，求点B的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

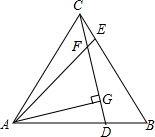    19．如图，等边三角形ABC中，DE分别是AB，BC边上的点，AD=BE，AE与CD相交于F，AG⊥CD，垂足为G，则sin∠AFG=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

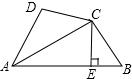    9．如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，且CD=CB，∠ABC+∠ADC=180°．求证：AE=$\frac{1}{2}$（AB+AD）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

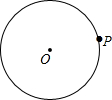    16．链球运动员在投掷链球时，链球按顺时针作圆周运动，如图，当运动员即将放手时，链球在⊙O的点P处．
    （1）链球将沿⊙O的切线方向飞出，请画出链球飞出的方向．
    （2）已知⊙O的半径OP为1.2m，假设链球在飞出的2s内方向不变，经过2s，链球飞出的距离为32m，求此时链球离点O的距离（精确到0.01m）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知∠AOB=50°，∠COB=30°，则∠AOC等于（　　）
    A．80°B．20°C．80°或20°D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．写出一个二次函数解析式，使它满足：①开口方向向下；②对称轴在y轴右侧；③与y轴相交于负半轴．y=-x2+x-1．

    查看答案和解析>>

    同步练习册答案