
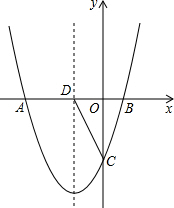
 如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点.
如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点.分析 (1)先由抛物线对称轴方程可求出b=2,再把点C(0,-2$\sqrt{3}$)代入y1=$\frac{1}{2}$x2+bx+c可得c=2$\sqrt{3}$,所以抛物线解析式为y1=$\frac{1}{2}$x2+2x-2$\sqrt{3}$;
(2)过O′点作O′H⊥x轴于H,如图1,由(1)得D(-2,0),C(0,2$\sqrt{3}$),在Rt△OCD中利用三角函数可计算出∠ODC=60°,再利用折叠的性质得O′D=OD=2,∠O′DC=∠ODC=60°,所以∠O′DH=60°,接着在Rt△O′DH中利用三角函数可计算出O′H=$\sqrt{3}$,利用勾股定理计算出DH=1,则O′(-3,-$\sqrt{3}$),然后根据二次函数图象上点的坐标特征判断O′点是否在抛物线y1上;
(3)①利用二次函数图象上点的坐标特征设E(m,$\frac{1}{2}$m2+2m-2$\sqrt{3}$)(m<0),过E作EH⊥x轴于H,连结DE,如图2,则DH=-2-m,EH=-$\frac{1}{2}$m2-2m+2$\sqrt{3}$,由(2)得∠ODC=60°,再利用轴对称性质得DC平分∠EDE′,DE=DE′,则∠EDE′=120°,所以∠EDH=60°,于是在Rt△EDH中利用三角函数的定义可得-$\frac{1}{2}$m2-2m+2$\sqrt{3}$=(-2-m)•$\sqrt{3}$,解得m1=2$\sqrt{3}$(舍去),m2=-4,则E(-4,-2$\sqrt{3}$),接着计算出DE=4,所以DE′=4,于是得到E′(2,0),然后计算x=2时得函数值即可得到F点坐标;
②由于点E关于直线CD的对称点E′恰好落在x轴,则PE=PE′,根据三角形三边的关系得|PE′-PF|≤E′F(当点P、E′F共线时,取等号),于是可判断直线CD上存在点P,使|PE-PF|最大,最大值为6-2$\sqrt{3}$.
解答 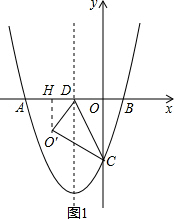 解:(1)∵抛物线对称轴x=-2,
解:(1)∵抛物线对称轴x=-2,
∴-$\frac{b}{2×\frac{1}{2}}$=-2,
解得b=2,
∵点C(0,-2$\sqrt{3}$)在抛物线y1=$\frac{1}{2}$x2+bx+c上,
∴c=2$\sqrt{3}$,
∴抛物线解析式为y1=$\frac{1}{2}$x2+2x-2$\sqrt{3}$;
(2)O点对称点O′不在抛物线y1上.理由如下:
过O′点作O′H⊥x轴于H,如图1,由(1)得D(-2,0),C(0,2$\sqrt{3}$),
在Rt△OCD中,∵OD=2,OC=$\sqrt{3}$,
∴tan∠ODC=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠ODC=60°,
∵△OCD沿CD翻折后,O点对称点O′,
∴O′D=OD=2,∠O′DC=∠ODC=60°,
∴∠O′DH=60°,
在Rt△O′DH中,sin∠O′DH=$\frac{O′H}{O′D}$,
∴O′H=2sin60°=$\sqrt{3}$,
∴DH=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∴O′(-3,-$\sqrt{3}$),
∵当x=-3时,y1=$\frac{1}{2}$x2+2x-2$\sqrt{3}$=$\frac{1}{2}$×9+2×(-3)-2$\sqrt{3}$≠-$\sqrt{3}$,
∴O′点不在抛物线y1上;
(3)①设E(m,$\frac{1}{2}$m2+2m-2$\sqrt{3}$)(m<0),
过E作EH⊥x轴于H,连结DE,如图2,则DH=-2-m,EH=-($\frac{1}{2}$m2+2m-2$\sqrt{3}$)=-$\frac{1}{2}$m2-2m+2$\sqrt{3}$,
由(2)得∠ODC=60°,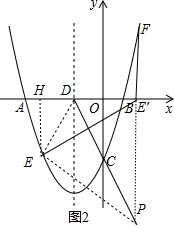
∵点E关于直线CD的对称点E′恰好落在x轴上,
∴DC垂直平分EE′,
∴DC平分∠EDE′,DE=DE′,
∴∠EDE′=120°,
∴∠EDH=60°,
在Rt△EDH中,∵tan∠EDH=$\frac{EH}{HD}$,
∴EH=HDtan60°,即-$\frac{1}{2}$m2-2m+2$\sqrt{3}$=(-2-m)•$\sqrt{3}$,
整理得m2+(4+2$\sqrt{3}$)m-8$\sqrt{3}$=0,解得m1=2$\sqrt{3}$(舍去),m2=-4,
∴E(-4,-2$\sqrt{3}$),
∴HD=2,EH=2$\sqrt{3}$,
∴DE=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
∴DE′=4,
∴E′(2,0),
而E′F⊥x轴,
∴F点的横坐标为2,
当x=2时,y1=$\frac{1}{2}$x2+2x-2$\sqrt{3}$=6-2$\sqrt{3}$,
∴F(2,6-2$\sqrt{3}$);
②∵点E关于直线CD的对称点E′恰好落在x轴,
∴PE=PE′,
∴|PE′-PF|≤E′F(当点P、E′F共线时,取等号),
∴直线CD上存在点P,使|PE-PF|最大,最大值为6-2$\sqrt{3}$.
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和折叠的性质;会运用三角函数进行几何计算;理解坐标与图形性质.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
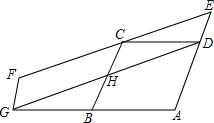 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24,24 | B. | 26,24 | C. | 28,26 | D. | 30,26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com