
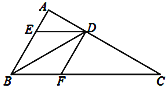
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
【答案】(1)证明见解析(2)25°
【解析】
(1)首先证明四边形DEBF是平行四边形,根据平行线的性质得到∠EDB=∠DBF,根据角平分线的性质得到∠ABD=∠DBF,等量代换得到∠ABD=∠EDB,得到DE=BE,即可证明四边形BEDF为菱形;
⑵根据三角形的内角和求出![]() 的度数,根据角平分线的性质得到
的度数,根据角平分线的性质得到![]() 的度数,根据平行线的性质即可求解.
的度数,根据平行线的性质即可求解.
(1)∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=![]() ∠ABC
∠ABC
∴∠ABD=∠EDB
∴DE=BE
∴四边形BEDF为菱形;
(2) ∠A=100°,∠C=30°,
![]()
∵BD平分∠ABC
∴∠ABD=∠DBF=![]() ∠ABC
∠ABC![]()
∵DE∥BC
∴∠EDB=∠DBF= 25°.


科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:

(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的![]() ;
;
(3)现有5名学生,其中A类型2名,B类型2名,从中任选2名学生参加很体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.8米,则这颗树的高度为_________米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C、点D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,连接AC、AD、BC,若∠ABD=2∠BDC.
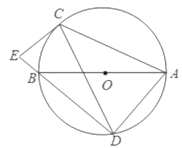
(1)求证:CE是⊙0的切线
(2)求证:△ABC![]() △CBE
△CBE
(3)若⊙O的半径为5,tan∠BDC=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com