
| A. | 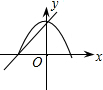 | B. | 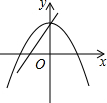 | C. |  | D. | 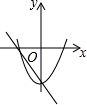 |
分析 可先根据一次函数的图象判断a、c的符号,再判断二次函数图象与实际是否相符,判断正误.
解答 解:A、由一次函数y=ax+c的图象可得:a>0,c>0,与x轴的交点坐标为(-$\frac{c}{a}$,0),与y轴的交点是(0,c),此时二次函数y=-ax2+c的图象应该开口向下,c>0,与x轴的交点坐标为(±$\frac{\sqrt{ac}}{a}$,0),与y轴的交点是(0,c),故A错误;
B、由一次函数y=ax+c的图象可得:a>0,c>0,与x轴的交点坐标为(-$\frac{c}{a}$,0),与y轴的交点是(0,c),此时二次函数y=-ax2+c的图象应该开口向下,c>0,与x轴的交点坐标为(±$\frac{\sqrt{ac}}{a}$,0),与y轴的交点是(0,c),故B正确;
C、由一次函数y=ax+c的图象可得:a<0,c>0,与x轴的交点坐标为(-$\frac{c}{a}$,0),与y轴的交点是(0,c),此时二次函数y=-ax2+c的图象应该开口向上,c<0,与x轴的交点坐标为(±$\frac{\sqrt{ac}}{a}$,0),与y轴的交点是(0,c),故A错误;
D、由一次函数y=ax+c的图象可得:a<0,c<0,与x轴的交点坐标为(-$\frac{c}{a}$,0),与y轴的交点是(0,c),此时二次函数y=-ax2+c的图象应该开口向上,c<0,与x轴的交点坐标为(±$\frac{\sqrt{ac}}{a}$,0),与y轴的交点是(0,c),故D错误;
故选:D.
点评 本题考查了二次函数图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com