
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
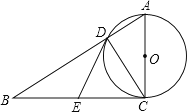
(1)求证:点E是边BC的中点;
(2)求证:BC2=BDBA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题(1)利用切线的性质及圆周角定理证明;
(2)利用相似三角形证明;
(3)利用正方形的性质证明.
试题解析:(1)如图,连接OD.
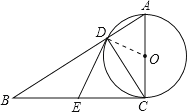
∵DE为切线,
∴∠EDC+∠ODC=90°;
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴ED=EC;
∵AC为直径,
∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,
∴∠B=∠BDE,
∴ED=BE.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,
∴∠ADC=∠ACB=∠BDC=90°,
又∵∠B=∠B
∴△ABC∽△CDB,
∴![]()
∴BC2=BDBA;
(3)当四边形ODEC为正方形时,∠OCD=45°;
∵AC为直径,
∴∠ADC=90°,
∴∠CAD=∠ADC-∠OCD=90°-45°=45°
∴Rt△ABC为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的角度为________.
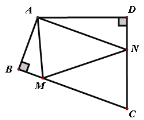
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5.
经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5.
(1)填空:点A的坐标为________;
(2)求双曲线和AB所在直线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com