
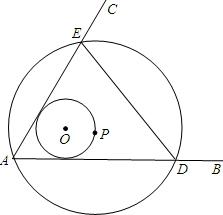
 如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.
如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$. 分析 当外接圆的半径最大时,△ADE的面积最大,连接AO并延长,与圆O交于P点,此时△ADE外接圆的半径最大,△ADE的面积最大,设圆O与AB相切于点M,连接OM,PD,由对称性得到AF为角平分线,得到∠FAD为30度,根据切线的性质得到OM垂直于AD,在直角三角形AOM中,利用30度角所对的直角边等于斜边的一半求出AO的长,由AO+OP求出AP的长,即为圆P的半径,由三角形AED为等边三角形,得到DP为角平分线,在直角三角形PFD中,利用30度所对的直角边等于斜边的一半求出PF的长,再利用勾股定理求出FD的长,由DE=2FD求出DE的长,可得△ADE的面积.
解答 解:连接AO并延长,与ED交于F点,与圆O交于P点,此时△ADE外接圆的半径最大,
连接OM,PD,可得F为ED的中点,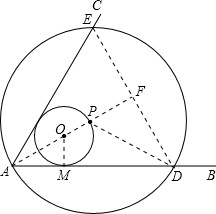
∵∠BAC=60°,AE=AD,
∴△AED为等边三角形,
∴AF为角平分线,即∠FAD=30°,
在Rt△AOM中,OM=1,∠OAM=30°,
∴OA=2,
∴PD=PA=AO+OP=3,
在Rt△PDF中,∠FDP=30°,PD=3,
∴PF=$\frac{3}{2}$,
根据勾股定理得:FD=$\sqrt{{PD}^{2}{-PF}^{2}}$=$\frac{3\sqrt{3}}{2}$,
DE=3$\sqrt{3}$,
∴S△ADE=$\frac{1}{2}×3\sqrt{3}×3\sqrt{3}×sin60°$=$\frac{27\sqrt{3}}{4}$,
故答案为:$\frac{27\sqrt{3}}{4}$.
点评 此题考查了切线的性质,等边三角形的判定与性质,勾股定理,含30度直角三角形的性质,熟练掌握切线的性质是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).
如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
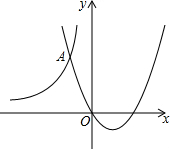 如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).
如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com