练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图所示，在一个水塘的表面均匀漂浮一些鱼食，一只小鱼正在A出，现在小鱼从A处出发到到水面取一点食物后，要回到岸边的B洞口处，画出小鱼这一过程中游动的最短路径（请保留作图中必要的辅助线）．

    分析 画出点A关于直线水面的对称点A′，连接A′B交水面于点D，连接AD，由对称的性质可知AD=A′D，由两点之间线段最短可知点D即为所求点．

    解答 解：作点A关于水面的对称点A′，连接A′B交水面于点D，连接AD，
    ∵点A与点A′关于水面对称，
    ∴AD=A′D，
    ∴AD+BD=A′B，
    由两点之间线段最短可知，线段A′B的长即为AD+BD的最小值，故D点即为所求点，其最短路径见下图：

    点评 本题考查的是轴对称路径最短问题，明确等点A′、D、B在一条直线上时路径最短是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．观察下面的一列单项式：2x，-4x2，8x3，-16x4…根据规律，第6个单项式为-64x6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知二次函数y=-x2+bx+c的图象的对称轴为直线x=-1，设图象与x轴交于点（x1，0）、（x2，0），若x12+x22=10，试求此函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，抛物线y=ax2+b与x轴交于点A，B，且A点的坐标为（1，0），与y轴交于点C（0，1）
    （1）求抛物线的表达式，并求出点B坐标；
    （2）过点B作BD∥CA，交抛物线与点D，连接BC，CA，AD，求四边形ACBD的周长（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

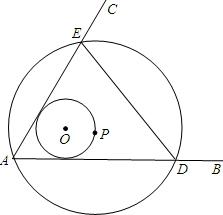    7．如图∠BAC=60°，半径长1的⊙0与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解不等式：x2-5x-5＞1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（-$\frac{2}{3}$）-（+$\frac{1}{3}$）-|-$\frac{3}{4}$|-（-$\frac{1}{4}$）
    （2）（-3）2÷2$\frac{1}{4}$×（-$\frac{3}{2}$）+4+22÷（-$\frac{8}{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在某复印社复印文件，复印页数不超过50时，每页收费0.11元，超过部分每页收费降为0.08元．在某图书馆复印同样的文件，不论复印多少页，每页收费0.09元．
    设需要复印文件x页（x为正整数），请根据表中提供的信息回答下列问题：
    （1）用含有x的式子填写如表：
    x≤50x＞50
    复印店计费/元0.11x0.08x+1.5
    图书馆计费/元0.09x0.09x
    （2）当x为何值时，两种收费相等；
    （3）当你有一本书要复印、页码共有200页，你认为在哪里复印省钱？（直接写出结果即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

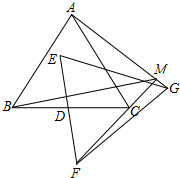    12．如图，△ABC、△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最大值是$\sqrt{3}$+1．

    查看答案和解析>>

    同步练习册答案