
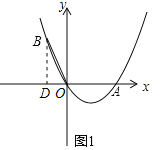
【题目】如图1,点A在x轴上,OA=4,将OA绕点O逆时针旋转120°至OB的位置.
(1)求经过A、O、B三点的抛物线的函数解析式;
(2)在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3 )如图2,OC=4,⊙A的半径为2,点M是⊙A上的一个动点,求MC+![]() OM的最小值.
OM的最小值.

【答案】(1)y=![]() x2﹣
x2﹣![]() x;(2)存在△POB为等腰三角形,符合条件的点P只有一个,坐标为(2,2
x;(2)存在△POB为等腰三角形,符合条件的点P只有一个,坐标为(2,2![]() );(3)MC+
);(3)MC+![]() OM的最小值为CK=5.
OM的最小值为CK=5.
【解析】
(1)设出抛物线解析式,利用待定系数法求出拋物线解析式即可
(2)设点P的坐标为(2,y),分三种情况讨论,①OB=OP,②2OB=PB,③OP=PB,分别求出y的值,即可得出点P的坐
(3)在OA上取点K,使AK=1,连接CK交圆与点M,连接OM、CM ,利用△AKM∽△AMO ,求出MC+![]() OM=MC+KM=CK,即可解答
OM=MC+KM=CK,即可解答
(1)如图1,过点B作BD⊥x轴于点D,
∴∠BDO=90°,
∵OA绕点O逆时针旋转120°至OB,
∴OB=OA=4,∠AOB=120°,B在第二象限,
∴∠BOD=60°,
∴sin∠BOD=![]() ,cos∠BOD=
,cos∠BOD=![]() ,
,
∴BD=![]() OB=2
OB=2![]() ,OD=
,OD=![]() OB=2,
OB=2,
∴B(﹣2,2![]() ),
),
设过点A(4,0),B(﹣2,2![]() ),O(0,0)的抛物线解析式为y=ax2+bx+c,
),O(0,0)的抛物线解析式为y=ax2+bx+c,
∴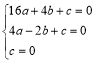 解得:
解得: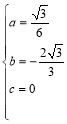 ,
,
∴抛物线的函数解析式为y=![]() x2﹣
x2﹣![]() x;
x;
(2)存在△POB为等腰三角形,
∵抛物线与x轴交点为A(4,0),O(0,0),
∴对称轴为直线x=2,
设点P坐标为(2,p),
则OP2=22+p2=4+p2,BP2=(2+2)2+(p﹣2![]() )2=p2﹣4
)2=p2﹣4![]() p+28,
p+28,
①若OP=OB=4,则4+p2=42
解得:p1=2![]() ,p2=﹣2
,p2=﹣2![]() ,
,
当p=﹣2![]() 时,∠POA=60°,即点P、O、B在同一直线上,
时,∠POA=60°,即点P、O、B在同一直线上,
∴p≠﹣2![]() ,
,
∴P(2,2![]() ),
),
②若BP=OB=4,则p2﹣4![]() p+28=42
p+28=42
解得:p1=p2=2![]() ,
,
∴P(2,2![]() );
);
③若OP=BP,则4+p2=p2﹣4![]() p+28,
p+28,
解得:p=2![]() ,
,
∴P(2,2![]() );
);
综上所述,符合条件的点P只有一个,坐标为(2,2![]() );
);
(3)在OA上取点K,使AK=1,连接CK交圆与点M,连接OM、CM,
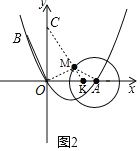
此时,MC+![]() OM=MC+KM=CK为最小值,
OM=MC+KM=CK为最小值,
理由:∵AK=1,MA=2,OA=4,
∴AM2=AKOA,而∠MAO=∠OAM,
∴△AKM∽△AMO,∴![]() =
=![]() ,
,
即:MC+![]() OM=MC+KM=CK,
OM=MC+KM=CK,
CK=![]() =5,
=5,
即:MC+![]() OM的最小值为CK=5.
OM的最小值为CK=5.


科目:初中数学 来源: 题型:
【题目】近年来,体育分数在中招考试中占分比重越来越大,不少家长、考生也越来越重视;某中学计划购买一批足球、跳绳供学生们考前日常练习使用,负责此次采购的老师从商场了解到:购买7个足球和4条跳绳共需510元;购买3个足球比购买5条跳绳少50元.
(1)求足球和跳绳的单价;
(2)按学校规划,准备购买足球和跳绳共200件,且足球的数量不少于跳绳的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
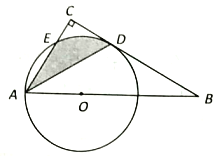
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好的了解中学生课外阅读的情况,学校团委将初一年级学生一学期阅读课外书籍量分为A(3本以内)、B(3——6本)、C(6——10本)、D(10本以上)四种情况进行了随机调查,并根据调查结果制成了如下两幅不完整的统计图.请结合统计图所给信息解答上列问题:
(1)在扇形统计图中C所占的百分比是多少?
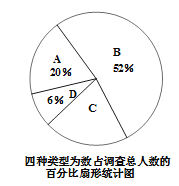
(2)请将折线统计图补充完整;

(3)学校团委欲从课外阅读量在10本以上的同学中随机邀请两位参加学校举办的“书香致远 墨卷至恒”主题读书日的形象大使,请你用列表法或画树状图的方法,求所选出的两位同学恰好都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
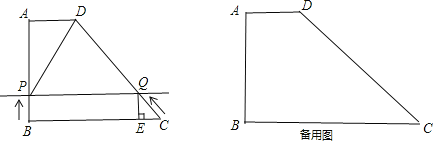
【题目】如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.
(1)求梯形ABCD的面积S;
(2)动点P从点B出发,以1cm/s的速度,沿BADC方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿CDA方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:
①当点P在BA上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;
②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;
③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
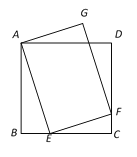
【题目】如图,已知正方形ABCD中,点E是BC上的一个动点,EF⊥AE交CD于点F,以AE,EF为边作矩形AEFG,若AB=4,则点G到AD距离的最大值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ![]() ,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
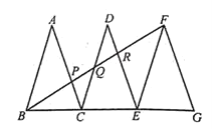
(1)求证:△BFG∽△FEG
(2)求sin∠FBG的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com