
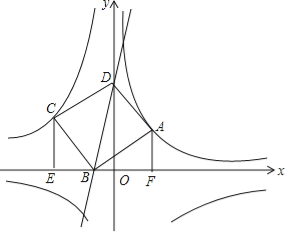
【题目】如图,点A(2,2)在双曲线y1=![]() (x>0)上,点C在双曲线y2=-
(x>0)上,点C在双曲线y2=-![]() (x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
(1)求k的值;
(2)求证:△BCE≌△ABF;
(3)求直线BD的解析式.
【答案】(1)4.(2)证明见解析.(3)y=5x+5.
【解析】
试题(1)把A点坐标代入y1=![]() 可求得k的值;
可求得k的值;
(2)由正方形的性质得出BC=AB,∠ABC=90°,再由角的互余关系证出∠BCE=∠ABF,由AAS即可证明△BCE≌△ABF;
(3)由△BCE≌△ABF得出BE=AF=2,CE=BF,设OB=x,则OE=x+2,CE=BF=x+2,点C的坐标为:(-x-2,x+2),代入双曲线y2=-![]() (x<0)得出方程:-(x+2)2=-9,得出x=1,OB=1,B(-1,0),AG=5,再由HL证明Rt△BOD≌Rt△CGA,得出OD=AG=5,得出D(0,5),设直线BD的解析式为:y=kx+b,把B、D坐标代入得出方程组,解方程组求出k、b,即可得出直线BD的解析式.
(x<0)得出方程:-(x+2)2=-9,得出x=1,OB=1,B(-1,0),AG=5,再由HL证明Rt△BOD≌Rt△CGA,得出OD=AG=5,得出D(0,5),设直线BD的解析式为:y=kx+b,把B、D坐标代入得出方程组,解方程组求出k、b,即可得出直线BD的解析式.
试题解析:(1)解:把点A(2,2)代入y1=![]() ,
,
得:2=![]() ,
,
∴k=4;
(2)证明:∵四边形ABCD是正方形,
∴BC=AB,∠ABC=90°,BD=AC,
∴∠EBC+∠ABF=90°,
∵CE⊥x轴,AF⊥x轴,
∴∠CEB=∠BFA=90°,
∴∠BCE+∠EBC=90°,
∴∠BCE=∠ABF,
在△BCE和△ABF中,
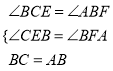 ,
,
∴△BCE≌△ABF;
(3)解:连接AC,作AG⊥CE于G,如图所示:
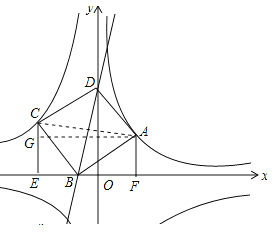
则∠AGC=90°,AG=EF,GE=AF=2,
由(2)得:△BCE≌△ABF,
∴BE=AF=2,CE=BF,
设OB=x,则OE=x+2,CE=BF=x+2,
∴OE=CE,
∴点C的坐标为:(-x-2,x+2),
代入双曲线y2=-![]() (x<0)得:-(x+2)2=-9,
(x<0)得:-(x+2)2=-9,
解得:x=1,或x=-5(不合题意,舍去),
∴OB=1,BF=3,CE=OE=3,
∴EF=2+3=5,CG=1=OB,B(-1,0),AG=5,
在Rt△BOD和Rt△CGA中,
![]() ,
,
∴Rt△BOD≌Rt△CGA(HL),
∴OD=AG=5,
∴D(0,5),
设直线BD的解析式为:y=kx+b,
把B(-1,0),D(0,5)代入得:![]() ,
,
解得:k=5,b=5.
∴直线BD的解析式为:y=5x+5.


科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,在BC边上取一点D,使CD=CA,点E在AC上,连接ED,若∠AED=45°,且CE=1,BD=2,则AD的长是 .
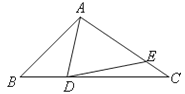
查看答案和解析>>
科目:初中数学 来源: 题型:
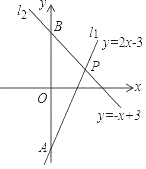
【题目】如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.
(1)求点P的坐标;
(2)点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)=________;
(3)试计算:101+103+…+197+199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,点P从点A向点D运动,点Q从点C向点B运动.已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,AD=4cm,BC=8cm,运动时间为t.当t=_____S时,四边形ABQP是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校需要置换一批推拉式黑板,经了解,现有甲、乙两厂家报价均为200元/米2,且提供的售后服务完全相同,为了促销,甲厂家表示,每平方米都按七折计费;乙厂家表示,如果黑板总面积不超过20米2,每平方米都按九折计费,超过20米2,那么超出部分每平方米按六折计费.假设学校需要置换的黑板总面积为x米2.
(1)请分别写出甲、乙两厂家收取的总费用y(元)与x(米2)之间的函数关系式;
(2)请你结合函数图象的知识帮助学校在甲、乙两厂家中,选择一家收取总费用较少的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会与实践的课堂上,刘老师组织七(1)班的全体学生用硬纸板制作圆柱体(图1).七(1)班共有学生50人,其中男生人数比女生人数少2人,并且每名学生每小时剪20个圆柱侧面(图2)或剪10个圆柱底面(图3).
(1)七(1)班有男生、女生各多少人?
(2)原计划男生负责剪圆柱侧面,女生负责剪圆柱底面,要求一个圆柱侧面配两个圆柱底面,那么每小时剪出的筒身与筒底能配套吗?如果不配套,那么男生应向女生支援多少人时,才能使每小时内剪出的侧面与底面配套.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第( )个图形有76个小圆.

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com