【题目】已知：甲、乙两车分别从相距300千米的A，B两地同时出发相向而行，甲到B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）请直接写出甲、乙两车离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数关系式，并标明自变量x的取值范围；
（2）它们在行驶的过程中有几次相遇？并求出每次相遇的时间．
【答案】
（1）解：甲由3小时到 
小时的速度是： 
=80千米/小时．
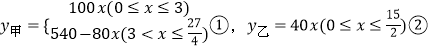
（2）解：由题意有两次相遇．
方法一：①当0≤x≤3时，100x+40x=300，解得 
，
②当 
时，（540﹣80x）+40x=300，解得x=6，
综上所述，两车第一次相遇时间为第 
小时，第二次相遇时间为第6小时．
方法二：设经过x小时两车首次相遇，
则40x+100x=300，解得 ，
设经过x小时两车第二次相遇，
则80（x﹣3）=40x，解得x=6．
综上所述，两车第一次相遇时间为第 小时，第二次相遇时间为第6小时．
【解析】（1）依图可知y甲的函数关系式为分段函数，y乙=40x，并标明自变量x的取值范围；
（2）如图可知甲与乙有两次相遇．再分段列方程求解即可得到答案．
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段CD是△ABC的“和谐分割线”，△ACD为等腰三角形 △CBD和△ABC相似，∠A =46°，则 ∠ACB的度数为 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书，途中小凡从路边超市买了一些学习用品，如图反应了他们俩人离开学校的路程
（千米）与时间
（分钟）的关系，请根据图象提供的信息回答问题：
（1）
和
中，__________描述小凡的运过程．
（2）___________谁先出发，先出发了___________分钟．
（3）___________先到达图书馆，先到了____________分钟．
（4）当
_________分钟时，小凡与小光在去学校的路上相遇．
（5）小凡与小光从学校到图书馆的平均速度各是多少千米/小时？（不包括中间停留的时间）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请先阅读下列文字与例题，再回答后面的问题：
当因式分解中，无法直接运用提取公因式和乘法公式时，我们往往可以尝试一个多项式分组后，再运用提取公因式或乘法公式继续分解的方法是分组分解法．
例如：
（1）
=
=
=
（2）
=
=
=
（1）根据上面的知识，我们可以将下列多项式进行因式分解：
(_____________)-(____________)=(_____________)-(____________)= (_____________)(_____________)；
=(_____________)+(____________)=(_____________)+(____________)= (_____________)(______________)．
（2）分解下列因式：
①
；
②
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，点M为边AD的中点，过点C作AB的垂线交AB于点E，连接ME，已知AM＝2AE＝4，∠BCE＝30°．
（1）求平行四边形ABCD的面积S；
（2）求证：∠EMC＝2∠AEM．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为（ ）
A.20海里
B.10 
海里
C.20 
海里
D.30海里
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某某摩托车厂本周计划每日生产
辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量，与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
根据记录回答：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
（1）本周三生产了多少摩托车？
（2）本周总生产量与计划生产量相比，是增加还是减少？
（3）产量最多的一天比产量最少的一天多生产了多少辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（背景知识）研究平面直角坐标系，我们可以发现一条重要的规律：若平面直角坐标系上有两个不同的点
、
，则线段AB的中点坐标可以表示为
（简单应用）如图1，直线AB与y轴交于点
，与x轴交于点
，过原点O的直线L将
分成面积相等的两部分，请求出直线L的解析式；
（探究升级）小明发现“若四边形一条对角线平分四边形的面积，则这条对角线必经过另一条对角线的中点”
如图2，在四边形ABCD中，对角线AC、BD相交于点O，
试说明
；
（综合运用）如图3，在平面直角坐标系中
，
，
，若OC恰好平分四边形OACB的面积，求点C的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
