
【题目】如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( )

A.m≥4B.m≤6C.4<m<6D.4≤m≤6
【答案】D
【解析】
根据题意可以作出合适的辅助线,然后根据题意,利用分类讨论的方法可以计算出m的两个极值,从而可以得到m的取值范围.
解:如图所示,
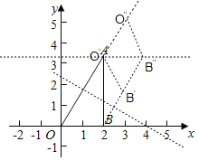
当直线l垂直平分OA时,O′B′和过A点且平行于x轴的直线有交点,
∵点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°,
∴∠BAO=30°,OB=2,
∴OA=4,
∵直线l垂直平分OA,点P(m,0)是直线l与x轴的交点,
∴OP=4,
∴当m=4;
作BB″∥OA,交过点A且平行于x轴的直线与B″,
当直线l垂直平分BB″和过A点且平行于x轴的直线有交点,
∵四边形OBB″O′是平行四边形,
∴此时点P与x轴交点坐标为(6,0),
由图可知,当OB关于直线l的对称图形为O′B′到O″B″的过程中,点P符合题目中的要求,
∴m的取值范围是4≤m≤6,
故选:D.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程.
(1)在方程![]() ①,
①,![]() ②,
②,![]() ③中,写出是不等式组
③中,写出是不等式组![]() 的相伴方程的序号 .
的相伴方程的序号 .
(2)写出不等式组![]() 的一个相伴方程,使得它的根是整数: .
的一个相伴方程,使得它的根是整数: .
(3)若方程![]() 都是关于
都是关于![]() 的不等式组
的不等式组![]() 的相伴方程,求
的相伴方程,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元/件的日用品。若按每件5元的价格出售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件;假定每月的销售件数y(万件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com