
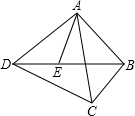
 E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.分析 (1)由三角形外角的性质及条件可得到∠AEB=∠ADC,结合条件可得到∠EAB=∠DAC,∠AEB=∠ADC,得出△ADC∽△AEB,根据相似三角形的性质即可得到结论;
(2)利用(1)的结论可证得△ADE∽△ACB,再利用相似三角形的性质可得出$\frac{BC}{ED}$=$\frac{AB}{AE}$=$\frac{AC}{AD}$.
解答 (1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠EAC=∠DAE+∠EAC.
∴∠EAB=∠DAC①;
又∵∠AEB=∠DAE+∠BDA=∠BDC+∠BDA,
∴∠AEB=∠ADC②;
由①和②得△AEB∽△ADC.
∴$\frac{BE}{CD}$=$\frac{AE}{AD}$;
(2)猜想:$\frac{BC}{DE}$=$\frac{AB}{AE}$或$\frac{BC}{DE}$=$\frac{AC}{AD}$.
证明:∵△AEB∽△ADC,
∴$\frac{AB}{AE}=\frac{AC}{AD}$,
∵∠BAC=∠DAE,
∴△BAC∽△EAD.
∴$\frac{BC}{ED}$=$\frac{AB}{AE}$=$\frac{AC}{AD}$.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,即①两个三角形的三边对应成比例、②两个三角形有两组角对应相等、③两个三角形的两组对边成比例且夹角相等,则这两个三角形相似.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
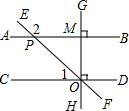
| A. | 130° | B. | 138° | C. | 140° | D. | 142° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<a<b<n | B. | a<m<n<b | C. | a<m<b<n | D. | m<a<n<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
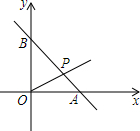 如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).
如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
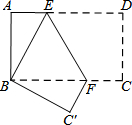 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
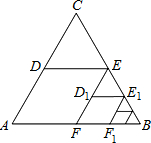 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20$\sqrt{3}$m | B. | $\frac{20\sqrt{3}}{3}$m | C. | 10$\sqrt{3}$m | D. | $\frac{40}{3}$$\sqrt{3}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com