
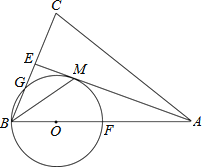
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线;
(2)当BC=8,AC=12时,求EM的长;
(3)在(2)的条件下,可求出⊙O的半径为 ,线段BG的长 .
【答案】(1)证明见解析;(2)![]() ;(3)3,2.
;(3)3,2.
【解析】
(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;
(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,由相似三角形的性质,可求出圆的半径,在直角三角形AEB中根据勾股定理可求出AE的长,再由平行线分线段成比例定理即可求出EM 的长;
(3)由(2)可知圆的半径为3,过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
(1)证明:连接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC,
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)设⊙O的半径为R,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() ,
,
∵AC=AB=12,
即![]() ,
,
解得R=3,
∴⊙O的半径为3,
∵OM∥BE,
∴AM:EM=AO:BO,
∵BE=4,AB=12,
∴AE=![]()
即![]() .
.
解得:EM=2![]() ;
;
(3)由(2)可知圆的半径为3,
过点O作OH⊥BG于点H,则BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.
故答案为:3,2.


科目:初中数学 来源: 题型:
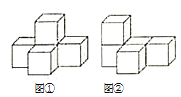
【题目】图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
A. 主视图,俯视较和左视图都改变
B. 左视图
C. 俯视图
D. 主视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.

(1)如图![]() ,点
,点![]() 、
、![]() 在
在![]() ,
,![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
(2)点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上,且
上,且![]() .
.
①如图![]() ,当点
,当点![]() 在
在![]() 的延长线上时,求证:
的延长线上时,求证:![]() ;
;
②当点![]() 在点
在点![]() ,
,![]() 之间,且
之间,且![]() 时,已知
时,已知![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家访是学校与家庭沟通的有效渠道,是形成教育合力的关键,是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中,教育局随机抽取了部分教师调查其近两周家访次数,将采集到的数据按家访次数分成五类,并分别绘制了下面的两幅不完整的统计图.
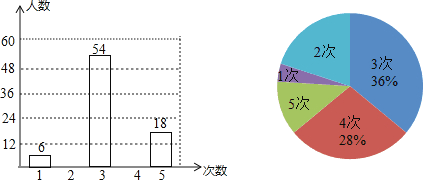
请根据以上信息,解答下列问题:
(1)请把条形统计图补充完整;
(2)所抽取的教师中,近两周家访次数的众数是 次,平均每位教师家访 次;
(3)若该市有12000名教师,请估计近两周家访不少于3次的教师有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
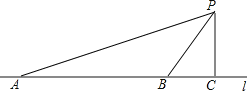
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
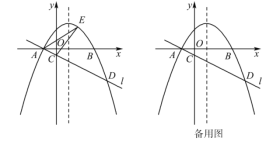
【题目】 如图所示,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求A,B两点的坐标及抛物线的对称轴;
(2)求直线l的函数解析式(其中k,b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(4)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
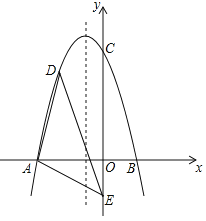
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
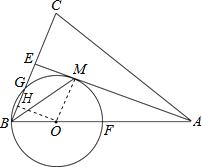
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com