
 某中学在一次爱心捐款活动中,全体同学积极踊跃捐款,抽查了九年级(1)班全班学生捐款情况,并绘制了如下的统计表和统计图:
某中学在一次爱心捐款活动中,全体同学积极踊跃捐款,抽查了九年级(1)班全班学生捐款情况,并绘制了如下的统计表和统计图:| 捐款(元) | 20 | 50 | 100 | 150 | 200 |
| 人数(人) | 4 | 12 | 9 | 3 | 2 |
分析 (Ⅰ)把表格中的数据相加得出本次接受随机抽样调查的学生人数;利用50元,100元的捐款人数求得占总数的百分比得出m、n的数值即可;
(Ⅱ)利用众数、中位数和平均数的意义和求法分别得出答案即可;
(Ⅲ)利用求得的平均数乘总人数得出答案即可.
解答 解:(Ⅰ)本次接受随机抽样调查的学生人数为4+12+9+3+2=30人.
12÷30=40%,9÷30=30%,
所以扇形统计图中的m=40,n=30;
(Ⅱ)∵在这组数据中,50出现了12次,次数最多,
∴学生捐款数目的众数是50;
∵按照从小到大排列,处于中间位置的两个数据都是50,
∴中位数为50;
这组数据的平均数=(20×4+50×12+100×9+150×3+200×2)÷30
=2430÷30
=81.
(Ⅲ)2500×81=202500元
答:估计该校学生共捐款202500元.
点评 此题考查扇形统计图,用样本估计总体,众数、中位数、平均数的意义与求法,理解题意,从图表中得出数据以及利用数据运算的方法是解决问题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:填空题
 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.若BC=10,则CF=$\frac{10}{3}$.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.若BC=10,则CF=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )| A. | x>-2 | B. | x>0 | C. | x<-2 | D. | x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
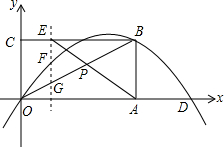 如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y=ax2+bx上,且抛物线交x轴于另一点D(6,0).
如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y=ax2+bx上,且抛物线交x轴于另一点D(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com