Question

4．如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．若BC=10，则CF=$\frac{10}{3}$．

Answer 1

分析 连结AF，如图，利用等腰三角形的性质和三角形内角和可计算出∠B=∠C=$\frac{1}{2}$（180°-∠BAC）=30°，再根据线段垂直平分线的性质得FA=FC，则∠FAC=∠C=30°，所以∠BAF=90°，然后在Rt△ABF中根据含30度的直角三角形三边的关系得到BF=2AF，则BF=2CF，所以3CF=10，于是得到CF=$\frac{10}{3}$．

解答 解：连结AF，如图，
∵AB=AC，
∴∠B=∠C=$\frac{1}{2}$（180°-∠BAC）=30°，
∵EF垂直平分AC，
∴FA=FC，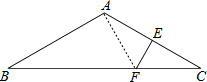
∴∠FAC=∠C=30°，
∴∠BAF=120°-30°=90°，
在Rt△ABF中，∵∠B=30°，
∴BF=2AF，
∴BF=2CF，
∴BC=3CF，即3CF=10，
∴CF=$\frac{10}{3}$．
故答案为$\frac{10}{3}$．

点评 本体考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．也考查了含30度的直角三角形三边的关系．