
【题目】如图,△ABC为等边三角形,AB=3,若点P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为_____.

【答案】![]()
【解析】
由等边三角形的性质得出∠ABC=∠BAC=60°,AC=AB=3,求出∠APC=120°,当PB⊥AC时,PB长度最小,设垂足为D,此时PA=PC,由等边三角形的性质得出AD=CD=![]() AC=
AC=![]() ,∠PAC=∠ACP=30°,∠ABD=
,∠PAC=∠ACP=30°,∠ABD=![]() ∠ABC=30°,求出PD=AD.tan30°=
∠ABC=30°,求出PD=AD.tan30°=![]() AD=
AD=![]() ,BD=
,BD=![]() AD=
AD=![]() ,即可得出答案.
,即可得出答案.
解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是![]() ,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=![]() AC=
AC=![]() ,∠PAC=∠ACP=30°,∠ABD=
,∠PAC=∠ACP=30°,∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∴PD=ADtan30°=![]() ×
×![]() =
=![]() ,
,
BD=![]() AD=
AD=![]() ,
,
∴PB=BD﹣PD=![]() ﹣
﹣![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
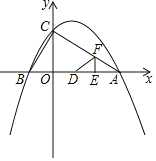
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”活动.经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,最终没有学生得分低于25分,也没有学生得满分.根据测试成绩绘制出频数分布表和频数分布直方图(如图).
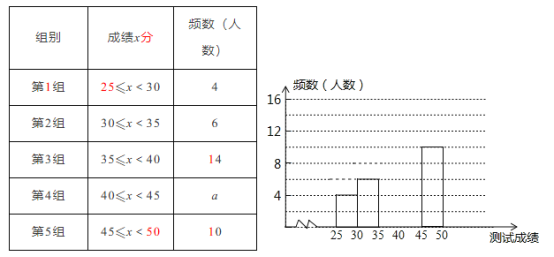
请结合图标完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若本次决赛的前5名是3名女生A、B、C和2名男生M、N,若从3名女生和2名男生中分别抽取1人参加市里的比赛,试用列表法或画树状图的方法求出恰好抽到女生A和男生M的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
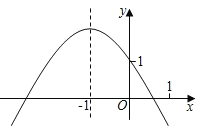
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
A.①②B.①③④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
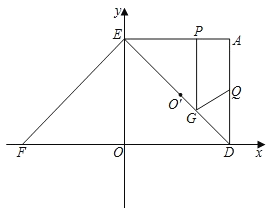
【题目】如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.
(1)求抛物线的解析式.
(2)过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.
(3)如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.
①若S=PQ2(厘米),试写出S与t之间的函数关系式,并写出t的取值范围?
②当S取最小时,在抛物线上是否存在点R,使得以P,A,Q,R为顶点的四边形是平行四边形?如果存在,求出R的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.
查看答案和解析>>
科目:初中数学 来源: 题型:
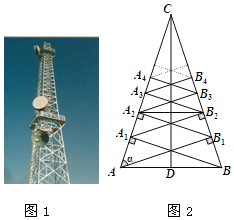
【题目】移动通信公司建设的钢架信号塔(如图1),它的一个侧面的示意图(如图2).CD是等腰三角形ABC底边上的高,分别过点A、点B作两腰的垂线段,垂足分别为B1,A1,再过A1,B1分别作两腰的垂线段所得的垂足为B2,A2,用同样的作法依次得到垂足B3,A3,….若AB为3米,sinα=![]() ,则水平钢条A2B2的长度为( )
,则水平钢条A2B2的长度为( )
A. ![]() 米B. 2米C.
米B. 2米C. ![]() 米D.
米D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教用品商店欲购进![]() 两种笔记本,用
两种笔记本,用![]() 元购进的
元购进的![]() 种笔记本与用
种笔记本与用![]() 元购进的
元购进的![]() 种笔记本的数量相同,每本
种笔记本的数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵
种笔记本的进价贵![]() 元,
元,
(1)求![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店![]() 种笔记本每本售价
种笔记本每本售价![]() 元,
元,![]() 种笔记本每本售价
种笔记本每本售价![]() 元,准备购进
元,准备购进![]() 两种笔记本共
两种笔记本共![]() 本,且这两种笔记本全部售出后总获利不少于
本,且这两种笔记本全部售出后总获利不少于![]() 元,则最多购进
元,则最多购进![]() 种笔记本多少本?.
种笔记本多少本?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com