
【题目】结合数轴与绝对值的知识回答下列问题:

(1)数轴上表示4和1的两点之间的距离是________;表示![]() 和2两点之间的距离是______;一般地,数轴上表示数
和2两点之间的距离是______;一般地,数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .如果表示数
.如果表示数![]() 和
和![]() 的两点之间的距离是3,那么
的两点之间的距离是3,那么![]() _______.
_______.
(2)若数轴上表示数![]() 的点位于
的点位于![]() 与2之间,求
与2之间,求![]() 的值;
的值;
(3)受(2)的启发,当数![]() 的点在图1什么位置时,
的点在图1什么位置时,![]() 的值最小,最小值是多少?
的值最小,最小值是多少?
(4)有理数![]() 、
、![]() 、
、![]() 在数轴上对应的位置如图2所示,试化简:
在数轴上对应的位置如图2所示,试化简:![]() .
.
【答案】(1) 3 , 5 ,![]() 或1;(2)6;(3)7;(4)3a-c
或1;(2)6;(3)7;(4)3a-c
【解析】
(1)根据两点间的距离公式即可求解;
(2)先计算绝对值,再合并同类项即可求解;
(3)受(2)的启发,可知当数a的点位于5与2之间位置时,|a+5|+|a2|的值最小,进一步得到最小值;
(4)利用绝对值的意义化简,再合并同类项即可求解.
(1)数轴上表示4和1的两点之间的距离是41=3;表示3和2两点之间的距离是2(3)=5;
依题意有|a(2)|=3,
解得a=5或1.
故填:3 , 5 ,![]() 或1;
或1;
(2)∵数a的点位于4与2之间,
∴|a+4|+|a2|
=a+4a+2
=6;
(3)当数a的点在图1的5与2之间位置时,|a+5|+|a2|的值最小,最小值是2(5)=7;
(4)依题意有ba<0,bc<0,a+b>0,ab>0,
则|ba||bc|+|a+b|+|ab|=b+a+bc+a+b+ab=3ac.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=![]() 的图象经过点C(3,m).
的图象经过点C(3,m).
(1)求菱形OABC的周长;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,
![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
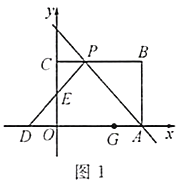
(1)如图1,若![]() 为等腰直角三角形,求直线
为等腰直角三角形,求直线![]() 的函数解析式;
的函数解析式;
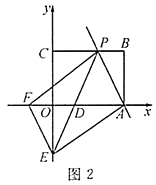
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若四边形
,若四边形![]() 是平行四边形,求直线
是平行四边形,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
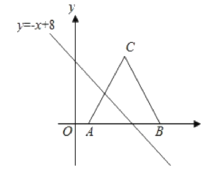
【题目】如图△ABC,AC=BC=13,把△ABC放在平面直角坐标系中,且点A、B的坐标分别为(2,0)、(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,农副产品也可以网上销售经过一段时间的精准帮扶,小张也建起了自家的网络商店(简称网店),他应用网店将种植的苹果和桃子销往全国各地.其中苹果每箱![]() 个
个![]() 以上的
以上的![]() 公斤左右包邮
公斤左右包邮![]() 元;桃子每箱
元;桃子每箱![]() 个
个![]() 公斤左右包邮
公斤左右包邮![]() 元.请你回答下列问题:
元.请你回答下列问题:
(1)网购一箱苹果和一箱桃子共应支付___________元;
(2)某社区重阳节慰问困难居民,计划在这家网店购买![]() 箱苹果和
箱苹果和![]() 箱桃子,应支付的费用可表示为______________________元;
箱桃子,应支付的费用可表示为______________________元;
(3)因为水果不耐贮存,小丽和两个同学合起来在这家网店购买了两箱苹果和一箱桃子,然后平均分配,小丽需支付多钱?她可以分到几个苹果和几个桃子?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠C=90°.
(1)已知 a=4![]() , b=2
, b=2![]() ,求 c ;
,求 c ;
(2)已知∠A=60°, c=2![]() +4,求 b ;
+4,求 b ;
(3)已知 a =10, c =10![]() ,求∠B;
,求∠B;
(4)已知 b =35,∠A=45°,求 a .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com