
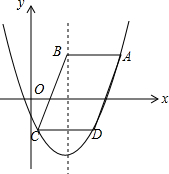
 如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示).
如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示). 分析 由抛物线解析式求出对称轴为x=2,得出点B的坐标,由已知条件得出AB,由平行四边形的性质得出CD=AB=m-2,设C的横坐标为x,则D的横坐标为x+m-2,由函数的对称性质得出方程$\frac{x+x+m-2}{2}$=2,求出x,即可得出点D的横坐标.
解答 解:∵抛物线y=a(x-2)2+k(a>0),
∴对称轴x=2,
∴B的横坐标为2,
∴AB=m-2,
∵四边形ABCD是平行四边形,
∴CD=AB=m-2,
设C的横坐标为x,
则D的横坐标为x+m-2,
∵C、D关于x=2对称,
∴$\frac{x+x+m-2}{2}$=2,
解得:x=$\frac{6-m}{2}$,
∴点D的横坐标为$\frac{6-m}{2}$+m-2=$\frac{m+2}{2}$;
故答案为:$\frac{m+2}{2}$.
点评 本题考查了平行四边形的性质、二次函数图象上点的坐标特征;熟练掌握平行四边形的性质,由函数的对称性得出方程是解决问题的关键.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
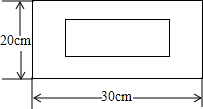 如图所示,有一块长方形土地,长为30m,宽为20m,在这块土地中按图中所示的方式修一条宽为a m的小路,余下的为菜地.
如图所示,有一块长方形土地,长为30m,宽为20m,在这块土地中按图中所示的方式修一条宽为a m的小路,余下的为菜地.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
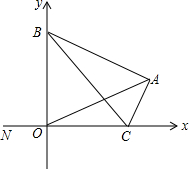 如图所示,在平面直角坐标系xOy中,△ABC的顶点B是y轴正半轴上一个定点,D是BO的中点.点C在x轴上,A在第一象限,且满足AB=AO,N是x轴负半轴上一点,∠BCN=∠BAO=α.
如图所示,在平面直角坐标系xOy中,△ABC的顶点B是y轴正半轴上一个定点,D是BO的中点.点C在x轴上,A在第一象限,且满足AB=AO,N是x轴负半轴上一点,∠BCN=∠BAO=α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明骑自行车从甲地到乙地.如图,折线表示小明途中所花时间t(h)与行程s(km)之间的函数关系.
小明骑自行车从甲地到乙地.如图,折线表示小明途中所花时间t(h)与行程s(km)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
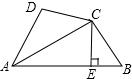 如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=$\frac{1}{2}$(AB+AD).
如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=$\frac{1}{2}$(AB+AD).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com