
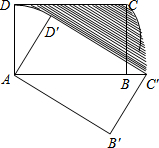
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 3 |
| 1 |
| 2 |
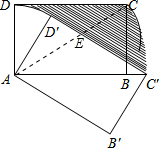 解:如图,连接AC.
解:如图,连接AC.| 3 |
| AD2+CD2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| απ×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| απ×12 |
| 360 |
| πα |
| 120 |
| πα |
| 120 |


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
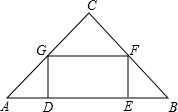 如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.
如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
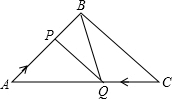 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△APQ |
| S△ABQ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | 60 | 65 | 70 | 75 | 80 | … |
| y | … | 60 | 55 | 50 | 45 | 40 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com