考点:圆周角定理,勾股定理,垂径定理,圆心角、弧、弦的关系
专题:
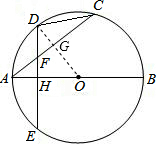
分析:(1)连接OD与AC相交于点G,判断出OD⊥AC,根据同弧所对的圆心角等于圆周角的2倍可得∠AOD=2∠DCF,再根据同角的余角相等求出∠AFH=∠AOD,然后求出∠DCF=∠AOD,即可得证;
(2)利用垂径定理求出DH,再根据等腰三角形两腰上的高相等可得AG=DH,然后求出△AFH和△AOG相似,再利用相似三角形对应边成比例列式求出AF,再根据FC=2AG-AF计算即可得解.
解答:(1)证明:连接OD与AC相交于点G,
则∠AOD=2∠DCF,
∵D为
的中点,
∴OD⊥AC,
又∵DE⊥AB,
∴∠A+∠AFH=∠A+∠AOG=90°,
∴∠AFH=∠AOD,
∵∠DFC=∠AFH,
∴∠DCF=∠AOD,
∴∠DFC=2∠DCF;
(2)解:∵DE⊥AB,AH=1,BH=4,
∴DH
2=AH•BH=1×4=4,
∴DH=2,
∵OD=OA,DE⊥OA,AG⊥OD,
∴AG=DH=2,
∵AH=1,BH=4,
∴AB=1+4=5,
∴AO=
AB=2.5,
∵DE⊥OA,AC⊥OD,
∴△AFH∽△AOG,
∴
=
,
即
=
,
解得AF=
,
∴FC=2AG-AF=2×2-
=
.
点评:本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,相似三角形的判定与性质,难点在于(2)利用相似三角形对应边成比例求出AF.

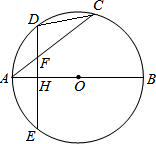 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为



