
 如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).
如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).分析 (1)由A、C两点坐标,利用待定系数法可求得抛物线解析式;
(2)由A、B关于对称轴对称,则可知PA=PB,则当P、B、C三点在一条线上时满足|PA-PC|最大,利用待定系数法可求得直线BC解析式,则可求得P点坐标;
(3)分AB为边和AB为对称线两种情况,当AB为边时,利用平行四边形的性质可得到CQ=AB,可得到关于D点的方程,可求得D点坐标,当AB为对角线时,则AB的中点也为CQ的中点,则可求得Q点坐标.
解答 解:
(1)∵二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4),
∴$\left\{\begin{array}{l}{-16-4b+c=0}\\{c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-3}\\{c=4}\end{array}\right.$,
∴二次函数的表达式为y=-x2-3x+4;
(2)∵y=-x2-3x+4,
∴对称轴为x=-$\frac{3}{2}$,
∵A(-4,0),
∴B(1,0),
∵P在对称轴上,
∴PA=PB,
∴|PA-PC|=|PB-PC|≤BC,即当P、B、C三点在一条线上时|PA-PC|的值最大,
设直线BC解析式为y=kx+b,
∴$\left\{\begin{array}{l}{k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-4}\\{b=4}\end{array}\right.$,
∴直线BC解析式为y=-4x+4,
令x=-$\frac{3}{2}$可得y=-4×(-$\frac{3}{2}$)+4=10,
∴存在满足条件的点P,其坐标为($-\frac{3}{2},10$);
(3)存在点Q,使A,B,C,Q四点构成平行四边形,
理由:①以AB为边时,则有CQ∥AB,即点Q的纵坐标为4,
∵CQ=AB=5,且C(0,4),
∴Q(-5,4)或(5,4),
②以AB为对角线时,CQ必过线段AB中点,且被AB平分,即:AB的中点也是CQ的中点,
∵A、B中点坐标为(-$\frac{3}{2}$,0),且C(0,4),
∴Q点横坐标=2×(-$\frac{3}{2}$)-0=-3,Q点纵坐标=0-4=-4,
∴Q(-3,-4),
综合可知存在满足条件的点D,坐标为(-5,4)或(5,4)或(-3,-4).
点评 本题为二次函数的综合应用,涉及待定系数法、轴对称的性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用步骤,在(2)中确定出点P的位置是解题的关键,在(3)中分AB为边和AB为对称线两种情况分别求解是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
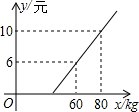 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com