
【题目】如图,△ABC中,AB=AC=2,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC=__________°;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由.

【答案】20
【解析】试题分析:(1)利用三角形的外角的性质得出答案即可;
(2)利用∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC得出∠BAD=∠EDC,进而求出△ABD≌△DCE;
(3)根据等腰三角形的判定以及分类讨论得出即可.
试题解析:(1)∵∠BAD=20°,∠B=40°,
∴∠ADC=60°,
∵∠ADE=40°,
∴∠EDC=60°-40°=20°.
(2)当DC=2时,△ABD≌△DCE;
理由:∵∠ADE=40°,∠B=40°,
又∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC.
∴∠BAD=∠EDC.
在△ABD和△DCE中,
 .
.
∴△ABD≌△DCE(ASA);
(3)当∠BAD=30°时,
∵∠B=∠C=40°,∴∠BAC=100°,
∵∠ADE=40°,∠BAD=30°,
∴∠DAE=70°,
∴∠AED=180°-40°-70°=70°,
∴DA=DE,这时△ADE为等腰三角形;
当∠BAD=60°时,∵∠B=∠C=40°,∴∠BAC=100°,
∵∠ADE=40°,∠BAD=60°,∠DAE=40°,
∴EA=ED,这时△ADE为等腰三角形.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
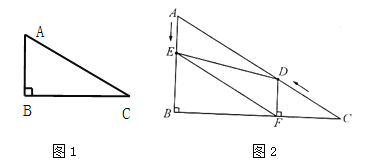
【题目】如图1,在Rt△ABC中,∠B=90°,∠C=30°.
(1)求证:AB=![]() AC;并请你用文字叙述直角三角形的这条性质,把它写在下列横线上:
AC;并请你用文字叙述直角三角形的这条性质,把它写在下列横线上:
;
(2)利用(1)题所得结论继续解答下列问题:
如图2,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连结DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连结DE、EF.
①求证:四边形AEFD是平行四边形;
②当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=![]() , CD=2连接AC、AD、BD、BC,AD、CB分别交⊙O于E、F.
, CD=2连接AC、AD、BD、BC,AD、CB分别交⊙O于E、F.
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是( )
成绩(分) | 9.2 | 9.3 | 9.4 | 9.5 | 9.6 |
人数 | 3 | 2 | 3 | 1 | 1 |
A. 中位数是9.4分B. 中位数是9.35分
C. 众数是3和1D. 众数是9.4分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点P(-2,a), Q(-2,a-5),若△POQ是直角三角形,则点P的坐标不可能为( )
A. (-2,4 )B. (-2, 0)C. (-2, 5)D. (-2,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com