
【题目】(9分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有![]() 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

【答案】(1)18;![]() (2)选择第一种方式来摆餐桌,理由见解析.
(2)选择第一种方式来摆餐桌,理由见解析.
【解析】
试题分析:(1)根据所给的例子可得有4张桌子,用第一种摆设方式,可以坐18人;1张桌子按第二种摆设方式可坐4+2=6人,2张桌子按第二种摆设方式可坐4+2×2=8人,3张桌子按第二种摆设方式可坐4+2×3=10人, 所以n张桌子按第二种摆设方式可坐4+2×n=![]() 人;(2)分别计算20张这样的长方形桌子按两种方式可坐的人数,比较大小即可.
人;(2)分别计算20张这样的长方形桌子按两种方式可坐的人数,比较大小即可.
试题解析:(1)18;![]() 4分(每格2分)
4分(每格2分)
(2)解:选择第一种方式来摆餐桌. 5分
理由如下:
∵第一种方式,4张桌子拼在一起可坐18人.
20张桌子可拼成5张大桌子,共可坐:![]() (人).
(人).
第二种方式,4张桌子拼在一起可坐12人.
20张桌子可拼成5张大桌子,共可坐:![]() (人). 7分
(人). 7分
又∵90>85>60
∴应选择第一种方式来摆餐桌. 9分


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.

⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;
⑵你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①画出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, ![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD, DE,直接写出△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接OC、BC、CE. 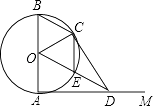
(1)求证:CD是⊙O的切线;
(2)若圆O的直径等于2,填空: ①当AD=时,四边形OADC是正方形;
②当AD=时,四边形OECB是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对函数y=x+ ![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | m | ﹣2 | ﹣ | ﹣ |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 , m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现: ①方程x+ ![]() =3有个实数根;
=3有个实数根;
②若关于x的方程x+ ![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 . 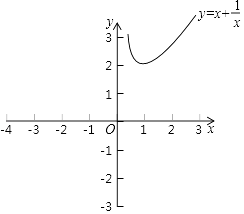
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表: 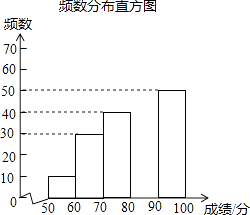
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= , n=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com