
【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.
科目:初中数学 来源: 题型:
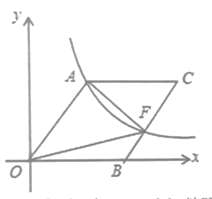
【题目】如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= ![]() 的图像与BC交于点F,则△AOF的面积为 ______________.
的图像与BC交于点F,则△AOF的面积为 ______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是BC上方抛物线上的动点,连接OD、CD,OD交BC于点F,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,点E的坐标为![]() ,在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请求出符合条件的点P的横坐标;若不存在,请说明理由.
,在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请求出符合条件的点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.以下五个结论:①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线y=4x+4分别与x 轴 ,y 轴分别交于A,B,点A在抛物线y=ax2+bx﹣3a (a<0)上,将点B向右平移3个单位长度,得到点C.
(1)求抛物线的顶点坐标;(用含a的代数式表示)
(2)若a=﹣1,当t﹣1≤x≤t时,函数y=ax2+bx﹣3a (a<0)的最大值是3,求t的值;
(3)若抛物线与线段BC有两个公共点,结合函数图像直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰 Rt△ABC 中,AC=BC= 2![]() ,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
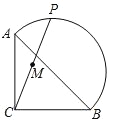
A. 2 B. 2 ![]() C. π D.
C. π D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°.
(1)按要求尺规作图,保留作图痕迹
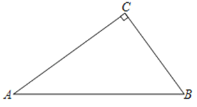
①作∠ABC平分线交AC于F点,
②作BF的垂直平分线交AB于M,以MB为半径作圆⊙M;
(2)在(1)所作图形中,证明⊙M与边AC相切;
(3)在(1)所作图形中,若∠CFB=∠CBA,BC=3,求⊙M的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘雨泽和黎昕两位同学玩抽数字游戏.五张卡片上分别写有2、4、6、8、![]() 这五个数字,其中两张卡片上的数字是相同的,从中随机抽出一张,已知
这五个数字,其中两张卡片上的数字是相同的,从中随机抽出一张,已知![]() (抽到数字4的卡片)
(抽到数字4的卡片)![]() .
.
(1)求这五张卡片上的数字的众数;
(2)若刘雨泽已抽走一张数字2的卡片,黎昕准备从剩余4张卡片中抽出一张.
①所剩的4张卡片上数字的中位数与原来5张卡片上数字的中位数是否相同?并简要说明理由;
②黎昕先随机抽出一张卡片后放回,之后又随机抽出一张,用列表法(或树状图)求黎昕两次都抽到数字4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com