
【题目】在Rt△ABC中,∠C=90°.
(1)按要求尺规作图,保留作图痕迹
①作∠ABC平分线交AC于F点,
②作BF的垂直平分线交AB于M,以MB为半径作圆⊙M;
(2)在(1)所作图形中,证明⊙M与边AC相切;
(3)在(1)所作图形中,若∠CFB=∠CBA,BC=3,求⊙M的半径.
【答案】(1)①作图见解析;②作图见解析;(2)证明见解析;(3)![]()
【解析】
(1)①根据尺规作图过程作∠ABC平分线交AC于F点即可;②作BF的垂直平分线交AB于M,以MB为半径做⊙M即可;
②作BF的垂直平分线交AB于M,以MB为半径作圆⊙M与边AC相切;
(2)在(1)所作图形中,根据切线的判定得出FM⊥AC,即可证明⊙M与边AC相切;
(3)在(1)所作图形中,根据∠CFB=∠CBA,BC=3,角平分线的性质,求出∠A的度数,即可求⊙M的半径.
解:(1)如图所示①BF即为所求;
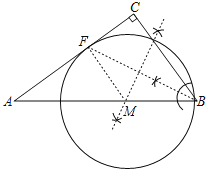
②如图所示⊙M为所求;
(2)证明:∵M在BF的垂直平分线上,
∴MF=MB,
∴∠MBF=∠MFB,
又∵BF平分∠ABC,
∴∠MBF=∠CBF,
∴∠CBF=∠MFB,
∴MF∥BC,
∵∠C=90°,
∴FM⊥AC,
∴⊙M与边AC相切;
(3)∵∠CFB=∠CBA,
∴∠A=∠CBF,
∴∠A=∠CBF=∠ABF,
∴∠A=30°,
∵BC=3,
∴AB=6,
设⊙M的半径为x,
∴MF=MB=x,则AM=2x,
∵MB+AM=AB,
∴3x=6,
∴x=2,
∴⊙M的半径为2.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫格点,![]() 的顶点都在格点上,仅用无刻度的直尺在网格中画图(保留作图连线痕迹),并回答问题.
的顶点都在格点上,仅用无刻度的直尺在网格中画图(保留作图连线痕迹),并回答问题.
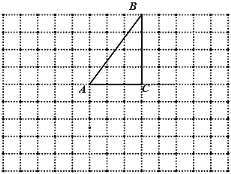
(1)在![]() 的右边找格点
的右边找格点![]() ,连
,连![]() ,使
,使![]() 平分
平分![]() .
.
(2)若![]() 与
与![]() 交于
交于![]() ,直接写出
,直接写出![]() 的值.
的值.
(3)找格点![]() ,连
,连![]() ,使
,使![]() 于
于![]() .
.
(4)在![]() 上找点
上找点![]() ,连
,连![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 轴于点
轴于点![]() ,且
,且![]() .
.
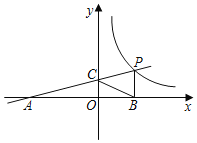
(1)求一次函数和反比例函数的解析式;
(2)点![]() 为反比例函数图象上使得四边形
为反比例函数图象上使得四边形![]() 为菱形的一点,点
为菱形的一点,点![]() 为
为![]() 轴上的一动点,当
轴上的一动点,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.
查看答案和解析>>
科目:初中数学 来源: 题型:
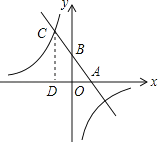
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
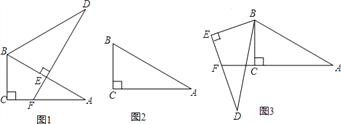
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如图.
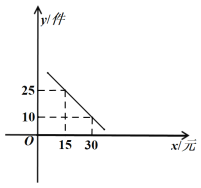
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为多少元时,此时每日的销售利润最多,最多是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() ,抛物线
,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
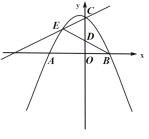

备用图
(1)求抛物线的解析式.
(2)点![]() 是直线
是直线![]() 上方的抛物线上一点,连接
上方的抛物线上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 与
与![]() 轴交于
轴交于![]() .
.
①点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,当以
,当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,求出线段
相似时,求出线段![]() 的长;
的长;
②点![]() 为
为![]() 轴左侧抛物线上一点,过点
轴左侧抛物线上一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
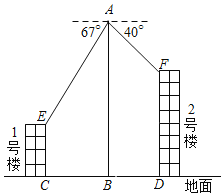
【题目】在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com