
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.以下五个结论:①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.

【答案】①④⑤
【解析】
先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x=![]() =
=![]() =1,
=1,
即2a+b=0;
故①正确;
②由抛物线的开口方向向上可推出a>0,而![]() >0
>0
∴b<0,
∵对称轴x=1,
∴当x=1时,y<0,
∴a+b+c<0;
故②错误;
③∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∴5a+b+c=0,
∴a+4a+b+c=0,
∵a>0,
∴4a+b+c<0,
故③错误;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0即a﹣b+c=0;
x=3时y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=![]() ,c=﹣
,c=﹣![]() ;
;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]()
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤正确.
故答案为:①④⑤.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙四边形”.
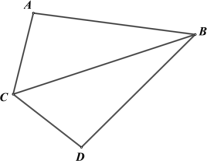
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABDC就称为“美妙四边形”.
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形,其中是“美妙四边形”的有 个;
(2)四边形ABCD是“美妙四边形”,AB=![]() ∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,我市某中学举行了“走进经典”征文比赛,赛后整理参赛学生的成绩,将学生的成绩分为![]() 四个等级,并将结果绘制成不完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
四个等级,并将结果绘制成不完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
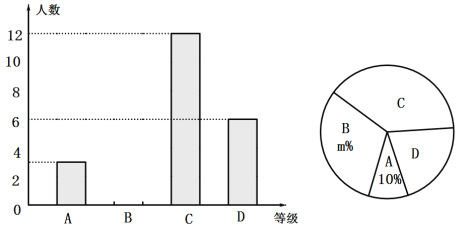
(1)参加征文比赛的学生共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,表示![]() 等级的扇形的圆心角为__ 图中
等级的扇形的圆心角为__ 图中![]() ;
;
(4)学校决定从本次比赛获得![]() 等级的学生中选出两名去参加市征文比赛,已知
等级的学生中选出两名去参加市征文比赛,已知![]() 等级中有男生一名,女生两名,请用列表或画树状图的方法求出所选两名学生恰好是一名男生和一名女生的概率.
等级中有男生一名,女生两名,请用列表或画树状图的方法求出所选两名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.
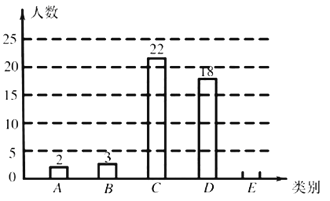
根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
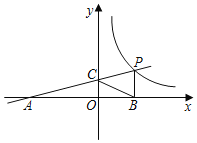
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)点![]() 为反比例函数图象上使得四边形
为反比例函数图象上使得四边形![]() 为菱形的一点,点
为菱形的一点,点![]() 为
为![]() 轴上的一动点,当
轴上的一动点,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
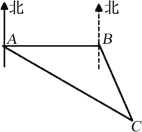
【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.
查看答案和解析>>
科目:初中数学 来源: 题型:
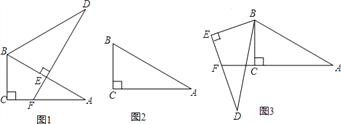
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.![]() 为抛物线上一动点(不与点
为抛物线上一动点(不与点![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方时,过点
上方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,请直接写出点
为顶点的四边形能否构成平行四边形?若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com