
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.

(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=2![]() .
.
【解析】
(1)易得∠BAD=90°,∠AED=90°,根据余角的性质得∠BAE=∠ADE,结合等腰三角形的性质和圆周角定理,即可得到结论;
(2)由正切函数的定义得AB=![]() AD, AG=
AD, AG=![]() AB,从而得AG=2AD,即点D为AG的中点,进而得DH∥AF,结合∠AED=90°,即可得到结论;
AB,从而得AG=2AD,即点D为AG的中点,进而得DH∥AF,结合∠AED=90°,即可得到结论;
(3)根据正切三角函数的定义和勾股定理得AB=6,BD=3![]() ,结合三角形的面积公式,即可得到答案.
,结合三角形的面积公式,即可得到答案.
(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠BAE+∠DAE=90°,
∵AE⊥BD,
∴∠AED=90°,
∴∠DAE+∠ADE=90°,
∴∠BAE=∠ADE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ACB=∠ADE,
∴∠ABC=∠ADE=∠BAE,
∴FA=FB;
(2)由(1)知,∠ABC=∠ACB=∠ADB,
∵tan∠ACB=![]() ,
,
∴tan∠ABC=tan∠ADB=![]() ,
,
又∵∠BAD=90°,
∴在Rt△BAD中,AB=![]() AD,在Rt△BAG中,AG=
AD,在Rt△BAG中,AG=![]() AB,
AB,
∴AG=![]() (
(![]() AD)=2AD,
AD)=2AD,
∴点D为AG的中点,
又∵点H为FG的中点,
∴DH∥AF,
由(1)知,∠AED=90°,
∴∠HDE=∠AED=90°,
∴DH⊥OD,
∴DH为⊙O的切线;
(3)∵AD=3![]() ,
,
∴AB=![]() AD=6,
AD=6,
∴在Rt△ABD中,BD=![]() =3
=3![]() ,
,
∵S△ABD=![]() ABAD=
ABAD=![]() BDAE,
BDAE,
∴6×3![]() =3
=3![]() ×AE,
×AE,
∴AE=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
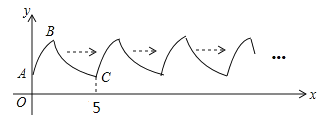
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
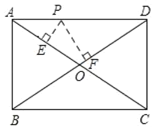
A.6B.12C.24D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量某建筑物AB的高度,在离该建筑物底部20m的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为38.5°,目高CD为1.6m.求建筑物AB的高度.(结果精确到1m)(参考数据:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
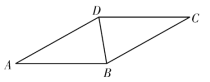
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E,DF 平分∠ADC 交边 BC 于 F,若 AD=11,EF=5,则 AB= ___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com