
����Ŀ��Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
������� | ���� | ռ���������� |
���� | 60 | m |
�赸 | 30 | 0.25 |
������ | n | 0.15 |
���� | 12 | 0.1 |
��1��������������������m��n��ֵ��
��2���벹ȫͳ��ͼ��
��3���������60��ϲ������ͬѧ����3����ϲ����������У��3000��ѧ��������Ƹ�У��ϲ�������������
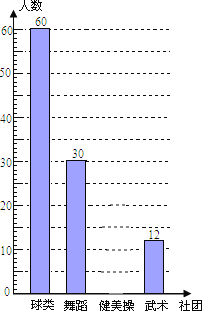
���𰸡���1��120,0.5,18����2���𰸼���������3��75.
��������
��1������ϲ����������12�ˣ���ռ�ı�����0.1���������������
��2�����ݣ�1���Ľ�������ɲ�ȫͳ��ͼ��
��3������������3000���Զ�Ӧ�ı��������ɹ��Ƹ�У��ϲ�������������
��1������������12��0.1��120��
m��60��120��0.5��n��120��0.15��18��
��2����ͼ��ʾ��
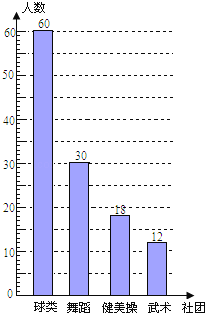 ��
��
��3��ѧУϲ���������У�3000��0.5��![]() ��75���ˣ���
��75���ˣ���
�𣺹��Ƹ�У��ϲ�����������Ϊ75��


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˾��345̨������Ҫһ�������͵�ijѧУ���ƻ����üס������ֻ�����8����֪ÿ�����ֻ���һ��������͵���45̨�������Ϊ400Ԫ��ÿ�����ֻ���һ��������͵���30̨�������Ϊ280Ԫ
���������ü��ֻ���![]() ����
����![]() Ϊ�Ǹ�������������д�±�.
Ϊ�Ǹ�������������д�±�.
��һ��
���ü��ֻ���������/�� | 3 | 7 |
|
���õļ��ֻ���������͵��Ե�����/̨ | 135 | ||
���õ����ֻ���������͵��Ե�����/̨ | 150 |
������
���ü��ֻ���������/�� | 3 | 7 |
|
���ü��ֻ����ķ���/Ԫ | 2800 | ||
�������ֻ����ķ���/Ԫ | 280 |
����������ɴ���������������ʡ���õ����������˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�����������Ϸ�����Ƕ�����һ���µĹ����þ����е������������������������������Ƚϴ�С������6�����ӣ��ֱ�Ϊ1������������2������������3������������Ϸ�������£�����Ϸʱ�����巴�泯�ϣ������������һ�����ӽ��б������������������岻�Żأ�����������ʤ������������������ʤ������������������ʤ��������������ͬ���Ӳ���ʤ����
��1����С����������С���������ų������¼��� ����С��������������������С����ʣ���5�������������һ��������һ����С��ʤС�Եĸ���Ϊ ��
��2�����������һ��������������ʣ���5��������С������һ�����ӣ�Ȼ��С����ʣ���4�������������һ��������һ����С����ʤ�ĸ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij��ѧ�С��ѡ������Сɽ�Ϸ�ij�ź���PQ�ĸ߶ȣ�������A������ź�������P������Ϊ45�����ź����Ͷ�Q������Ϊ31������ˮƽ������ǰ��100����������ź�������P������Ϊ68�������ź���PQ�ĸ߶ȣ��������ȷ��0.1�ף��ο����ݣ�sin68��� 0.93��cos68�� �� 0.37��tan68�� �� 2.48��tan31�� �� 0.60��sin31�� �� 0.52��cos31���0.86��
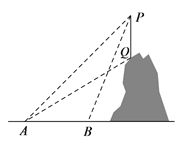
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��A����3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4���������2019��ֱ�Ƕ��������Ϊ��������
A. ��8076��0��B. ��8064��0��C. ��8076��![]() ��D. ��8064��
��D. ��8064��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��AB��AD���Խ���AC��BD���ڵ�O��ACƽ����BAD������C��CE��AB��AB���ӳ����ڵ�E������OE��
��1����֤���ı���ABCD�����Σ�
��2����AB��![]() ��BD��2����OE�ij���
��BD��2����OE�ij���
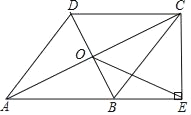
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������깺���֧����ʽ�������࣬ij��ѧ��ȤС��ʹ˽����˳������飮��������ʾ��֧����ʽ�У�A�š�B֧������C�ֽ�D��������С���ij����һ���ڹ����ߵ�֧����ʽ���е���ͳ�ƣ��õ�����������������ͳ��ͼ��

�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1������һ�������˶����������ߣ�
��2���벹ȫ����ͳ��ͼ��������ͳ��ͼ��A��֧����ʽ����Ӧ��Բ�Ľ�Ϊ�� ���ȣ�
��3�����ó�����һ������1600�������ߣ��������ʹ��A��B����֧����ʽ�Ĺ����߹��ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��y=��x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
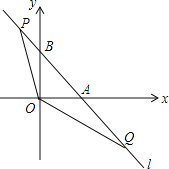
��1�����AOB���ܳ���
��2����AQ=t��0�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��3��������P��Q��ֱ��l���˶���ʹ�á�AOQ���BPO���ܳ����ʱ����tan��AOQ=m��������A�Ķ��κ���y=ax2+bx+cͬʱ������������������
��6a+3b+2c=0��
�ڵ�m��x��m+2ʱ������y�����ֵ����![]() ���������ϵ��a��ֵ��
���������ϵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У���ACB=90�㣬��BCΪֱ���ġ�O��AB�ڵ�D��EΪ![]() ���е�.
���е�.
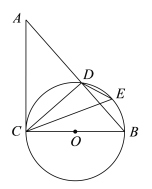
��1����֤����ACD=��DEC����2���ӳ�DE��CB���ڵ�P����PB=BO��DE=2����PE�ij�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com