
����Ŀ������ʮһ���ƽ����ڼ䣬ij�̵깺��һ���ʺ���Ʒ������Ϊ20Ԫ/ǧ�ˣ��ۼ۲�����20Ԫ/ǧ�ˣ��Ҳ�����32Ԫ/ǧ�ˣ�����������������ָú���Ʒһ���������y��ǧ�ˣ��������ۼ�x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ
������y��ǧ�ˣ� | �� | 34.8 | 32 | 29.6 | 28 | �� |
�ۼۣ�x����Ԫ/ǧ�ˣ� | �� | 22.6 | 24 | 25.2 | 26 | �� |
��1����գ������ֺ���Ʒ���ۼ�Ϊ30Ԫ/ǧ�ˣ���ú���Ʒ������������ ����
��2�����ij���������ֺ���Ʒ����150Ԫ����ô�������Ʒ���ۼ�Ϊ����Ԫ��
���𰸡���1��20;��2��25Ԫ��
��������
��1�����ݱ����е����ݣ����ô���ϵ���������y��x֮��ĺ�����ϵʽ��������һ�κ���ͼ���ϵ����������������������ۼ�Ϊ30Ԫ/ǧ��ʱ�ú���Ʒ����������
��2������������ÿǧ�˵��������������������ɵó�����x��һԪ���η��̣���֮���ɵó�x��ֵ������20��x��32������ȷ��x��ֵ������ý⣮
��1����y��x֮��ĺ�����ϵʽΪy��kx+b��k��0����
����24��32������26��28������y��kx+b���ã�
![]() ����ã�
����ã�![]()
��y��x֮��ĺ�����ϵʽΪy����2x+80��
��x��30ʱ��y����2��30+80��20��
�ʴ�Ϊ��20��
��2������������x��20������2x+80����150��
��ã�x1��25��x2��35��
��20��x��32��
��x��25��
�����ij���������ֺ���Ʒ����150Ԫ����ô�������Ʒ���ۼ�Ϊ25Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����������ת����ת���У�ָ��λ�ù̶����������ε��������ȣ��ҷֱ��������1��2��3��

��1��С��ת��ת��һ�Σ���ת��ֹͣת��ʱ��ָ����ָ�����е������������ĸ���Ϊ________��
��2��С����ת��ת��һ�Σ���ת��ֹͣת��ʱ����¼��ָ����ָ�����е����֣�������ת��ת��һ�Σ���ת��ֹͣת��ʱ���ٴμ�¼��ָ����ָ�����е����֣�������������֮����3�ı����ĸ���(�û���״ͼ���б��ȷ������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ax2+bx+c=0��a��0���ǹ���x��һԪ���η��̣�
��1��ֱ��д�����̸����б�ʽ��
��2��д�������ʽ���Ƶ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
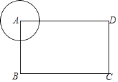
����Ŀ����ͼ������ABCD��AB=2��BC= ![]() ����A����AΪԲ�ģ��뾶r=1��Բ������A���ŵ�B˳ʱ����ת����ת��Ϊ���� 0�㣼����180����������ת���Բ�����ABCD�ı�����ʱ����=________�ȣ�
����A����AΪԲ�ģ��뾶r=1��Բ������A���ŵ�B˳ʱ����ת����ת��Ϊ���� 0�㣼����180����������ת���Բ�����ABCD�ı�����ʱ����=________�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ţ�̣�����Ϊÿ��24Ԫ���涨�ۼ۲����ڽ��ۣ����ڵ��ۼ�Ϊÿ��36Ԫ��ÿ�¿�����60�䣮�г����鷢�֣�������ţ�̵��ۼ�ÿ����1Ԫ����ÿ�µ�����������10�䣬��ÿ��ţ�̽���xԪ(xΪ������)��ÿ�µ�����Ϊy�䣮
��1��д��y��x�м�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������ζ��ۣ�����ʹÿ������ţ�̵����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���![]() �У�
��![]() ��
��![]() ����
����![]() �ǣ�
�ǣ�![]() ����ֱ�����ǰ�
����ֱ�����ǰ�![]() ����ͼ����ͼ��ƽ�ƣ�ֱ�DZ�
����ͼ����ͼ��ƽ�ƣ�ֱ�DZ�![]() ������
������![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ��ӳ�
�ϣ��ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ����
����![]() ��
��![]() �����
�����![]() �ӵ�
�ӵ�![]() ƽ�Ƶ���
ƽ�Ƶ���![]() �Ĺ����У���
�Ĺ����У���![]() ���˶�·����Ϊ__________��
���˶�·����Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
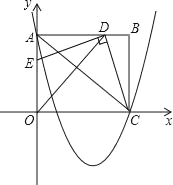
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��y����������ϣ�C��x����������ϣ���֪A��0��8����C��10��0��������AOC��ƽ���߽�AB�ڵ�D������CD������D��DE��CD��OA�ڵ�E��
��1�����D�����ꣻ
��2����֤����ADE�ա�BCD��
��3��������y��![]() x2��
x2��![]() x+8������A��C������AC��̽��������P��x���·���������һ���㣬����P��ƽ����y���ֱ�߽�AC�ڵ�M���Ƿ���ڵ�P��ʹ�߶�MP�ij��������ֵ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
x+8������A��C������AC��̽��������P��x���·���������һ���㣬����P��ƽ����y���ֱ�߽�AC�ڵ�M���Ƿ���ڵ�P��ʹ�߶�MP�ij��������ֵ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
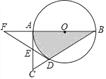
����Ŀ����ͼ����Rt��ABC�У���BAC=90������ABΪֱ������O��BC�ڵ�D��EΪAC���е㣬����DE���ӳ���BA���ӳ����ڵ�F��
��1����֤��DE�ǡ�O�����ߣ�
��2������F=30������O�İ뾶Ϊ2![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǻ�![]() ���е㣬��O������BD��AC���ӳ����ڵ�D,E��OB���е㣬CE���ӳ��߽�����BD�ڵ�F,AF����O�ڵ�H,����BH.
���е㣬��O������BD��AC���ӳ����ڵ�D,E��OB���е㣬CE���ӳ��߽�����BD�ڵ�F,AF����O�ڵ�H,����BH.
����֤��AC=CD.
����OB=2,��BH�ij�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com