
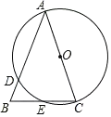
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求tan∠BAC的值.
【答案】(1)证明见解析;(2)tan∠BAC=![]() .
.
【解析】
(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE,进而利用等腰三角形的性质得出∠BAE=∠CAE,进而证明即可;
(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.
(1)证明:连结AE
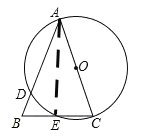
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
(2)连结DE,AE,CD则CD⊥AB,
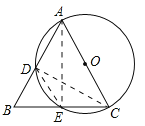
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴△BED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BA=9,
∴AC=BA=9.
∴AD=7,CD=![]() =
=![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:如果存在常数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ≤
≤![]() ,那么称这个函数是有上界函数;在所有满足条件的
,那么称这个函数是有上界函数;在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如,函数
中,其最小值称为这个函数的上确界.例如,函数![]() ,
, ![]() ≤2,因此是有上界函数,其上确界是2.如果函数
≤2,因此是有上界函数,其上确界是2.如果函数![]() (
(![]() ≤x≤
≤x≤![]() ,
, ![]() <
<![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过2
,且这个函数的最小值不超过2![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() ≤
≤![]() B.
B. ![]() C.
C. ![]() ≤
≤![]() D.
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英同时掷甲、乙两个质地均匀的骰子(6个面上分别标有1,2,3,4,5,6这6个数字).记甲朝上的一面数字为x,乙朝上的一面数字为y,这样确定点P的一个坐标(x,y),那么点P落在y=![]() 上的概率是_____.
上的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
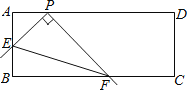
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
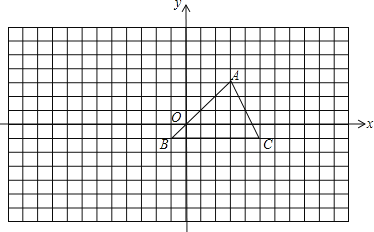
【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
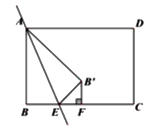
【题目】如图,矩形ABCD中,AB=5,BC=7,E为BC上的动点,将矩形沿直线AE翻折,使点B的对应点B'落在∠ADC的平分线上,过点B'作B'F⊥BC于点F,求△B'EF的周长______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P, AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com