
 如图,一个正六棱柱高为10cm,底面正六边形的边长为3cm.
如图,一个正六棱柱高为10cm,底面正六边形的边长为3cm.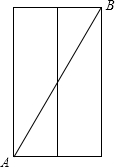 解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,
解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,| (3+3)2+102 |
| 34 |


科目:初中数学 来源: 题型:
 我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.| a+b |
| 2 |
| 2ab |
| a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 观察思考:
观察思考:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com