
ЁОЬтФПЁПвбжЊЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() (
(![]() ЃО0)ЕФЭМЯѓОЙ§ЕуC(0ЃЌ1)ЃЌЧвгы
ЃО0)ЕФЭМЯѓОЙ§ЕуC(0ЃЌ1)ЃЌЧвгы![]() жсНЛгкВЛЭЌЕФСНЕуAЁЂBЃЌЕуAЕФзјБъЪЧ(1ЃЌ0)ЃЎ
жсНЛгкВЛЭЌЕФСНЕуAЁЂBЃЌЕуAЕФзјБъЪЧ(1ЃЌ0)ЃЎ
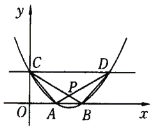
ЃЈ1ЃЉЧѓcЕФжЕКЭ![]() ЃЌ
ЃЌ![]() жЎМфЕФЙиЯЕЪНЃЛ
жЎМфЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИУЖўДЮКЏЪ§ЕФЭМЯѓгыжБЯп![]() НЛгкCЁЂDСНЕуЃЌЩш AЁЂBЁЂCЁЂDЫФЕуЙЙГЩЕФЫФБпаЮЕФЖдНЧЯпЯрНЛгкЕуPЃЌМЧЁїPCDЕФУцЛ§ЮЊS1ЃЌЁїPABЕФУцЛ§ЮЊS2ЃЌЕБ0ЃМ
НЛгкCЁЂDСНЕуЃЌЩш AЁЂBЁЂCЁЂDЫФЕуЙЙГЩЕФЫФБпаЮЕФЖдНЧЯпЯрНЛгкЕуPЃЌМЧЁїPCDЕФУцЛ§ЮЊS1ЃЌЁїPABЕФУцЛ§ЮЊS2ЃЌЕБ0ЃМ![]() ЃМlЪБЃЌЧѓжЄЃКS1ЃS2ЮЊГЃЪ§ЃЌВЂЧѓГіИУГЃЪ§ЃЎ
ЃМlЪБЃЌЧѓжЄЃКS1ЃS2ЮЊГЃЪ§ЃЌВЂЧѓГіИУГЃЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃО0ЃЌЧв
ЃО0ЃЌЧв![]() Ёй1ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌетИіГЃЪ§ЮЊ1
Ёй1ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌетИіГЃЪ§ЮЊ1
ЁОНтЮіЁП
ЃЈ1ЃЉЗжБ№НЋAЕуКЭCЕуЕФзјБъДњШы![]() МДПЩЕУНтЃЛ
МДПЩЕУНтЃЛ
ЃЈ2ЃЉИљОнЖўДЮКЏЪ§ЕФЖЈвхМАХаБ№ЪННјааЧѓНтМДПЩЕУЕНaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌЗжБ№ЧѓГі![]() ЕФУцЛ§S1МА
ЕФУцЛ§S1МА![]() ЕФУцЛ§ЮЊS2ЃЌДгЖјНјааЛЏМђМДПЩЕУНт.
ЕФУцЛ§ЮЊS2ЃЌДгЖјНјааЛЏМђМДПЩЕУНт.
ЃЈ1ЃЉНЋЕу![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
Ёр![]()
НЋЕу![]() ДњШыЕУ
ДњШыЕУ![]()
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкВЛЭЌЕФСНЕу
жсНЛгкВЛЭЌЕФСНЕу
ЁрвЛдЊЖўДЮЗНГЬ![]() ЕФХаБ№ЪН
ЕФХаБ№ЪН![]()
Жј![]()
Ёр![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃО0ЃЌЧв
ЃО0ЃЌЧв![]() Ёй1ЃЛ
Ёй1ЃЛ
ЃЈ3ЃЉжЄУїЃКЁп0ЃМ![]() ЃМ1
ЃМ1
ЁрЖдГЦжсЮЊ![]() ЃО1
ЃО1
Ёр![]()
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]()
Ёр![]()
![]()
Ёр![]() ЮЊГЃЪ§ЃЌетИіГЃЪ§ЮЊ1.
ЮЊГЃЪ§ЃЌетИіГЃЪ§ЮЊ1.


 УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ
ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ ШЋФмДГЙи100ЗжЯЕСаД№АИ
ШЋФмДГЙи100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
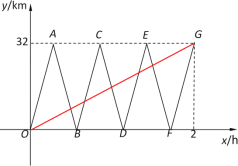
ЁОЬтФПЁПФГЙлЙтКўЗчОАЧјЃЌвЛЙлЙтТжгывЛбВТпЭЇЭЌЪБДгМзТыЭЗГіЗЂЪЛЭљввТыЭЗЃЌбВТпЭЇдШЫйЭљЗЕгкМзЁЂввСНИіТыЭЗжЎМфЃЌЕБЙлЙтТжЕНДяввТыЭЗЪБЃЌбВТпЭЇвВЭЌЪБЕНДяввТыЭЗЃЎЩшГіЗЂx hКѓЃЌЙлЙтТжЁЂбВТпЭЇРыМзТыЭЗЕФОрРыЗжБ№ЮЊy1 kmЁЂy2 kmЃЎЭМжаЕФЯпЖЮOGЁЂелЯпOABCDEFGЗжБ№БэЪОy1ЁЂy2 гыxжЎМфЕФКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉЙлЙтТжЕФЫйЖШЪЧ km/hЃЌбВТпЭЇЕФЫйЖШЪЧ km/hЃЛ
ЃЈ2ЃЉЧѓећИіЙ§ГЬжаЙлЙтТжгыбВТпЭЇЕФзюДѓОрРыЃЛ
ЃЈ3ЃЉЧѓећИіЙ§ГЬжаЙлЙтТжгыбВТпЭЇЯргіЕФзюЖЬЪБМфМфИєЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPBЮЊЁбOЕФЧаЯпЃЌBЮЊЧаЕуЃЌжБЯпPOНЛЁбгкЕуEЁЂFЃЌЙ§ЕуBзїPOЕФДЙЯпBAЃЌДЙзуЮЊЕуDЃЌНЛЁбOгкЕуAЃЌбгГЄAOгыЁбOНЛгкЕуCЃЌСЌНгBCЃЌAFЃЎ
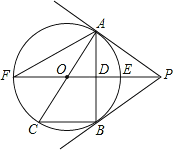
ЃЈ1ЃЉЧѓжЄЃКжБЯпPAЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЪдЬНОПЯпЖЮEFЁЂODЁЂOPжЎМфЕФЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ3ЃЉШєBC=6ЃЌtanЁЯF=![]() ЃЌЧѓcosЁЯACBЕФжЕКЭЯпЖЮPEЕФГЄЃЎ
ЃЌЧѓcosЁЯACBЕФжЕКЭЯпЖЮPEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГВшОпЕъЙКНјСЫAЁЂBСНжжВЛЭЌЕФВшОпЃЌ1ЬзAжжВшОпКЭ2ЬзBжжВшОпЙВаш250дЊЃЛ3ЬзAжжВшОпКЭ4ЬзBжжВшОпЙВаш600дЊЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНжжВшОпУПЬзЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉгЩгкВшОпГЉЯњЃЌВшОпЕъзМБИдйЙКНјAЁЂBСНжжВшОпЙВ80ЬзЃЌЕЋетДЮНјЛѕЪБЃЌЙЄГЇЖдAжжВшОпУПЬзНјМлЬсИпСЫ8%ЃЌЖјBжжВшОпУПЬзАДЕквЛДЮНјМлЕФАЫелЃЌШєВшОпЕъБОДЮНјЛѕзмЧЎЪ§ВЛГЌЙ§6240дЊЃЌдђзюЖрПЩНјAжжВшОпМИЬзЃП
ЃЈ3ЃЉШєЯњЪлвЛЬзAжжВшОпПЩЛёРћ30дЊЃЌЯњЪлвЛЬзBжжВшЦфПЩЛёРћ20дЊЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчКЮНјЛѕПЩЪЙБОДЮЙКНјВшОпЛёРћзюЖрЃПзюЖрЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫзМБИећРэвЛХњаТЕНЕФЪЕбщЦїВФЃЌШєМзЕЅЖРећРэашвЊ40ЗжжгЭъЙЄЃЌШєМзЁЂввЙВЭЌећРэ20ЗжжгКѓЃЌввашдйЕЅЖРећРэ20ЗжжгВХФмЭъЙЄ.
ЂХЮЪввЕЅЖРећРэЖрЩйЗжжгЭъЙЄЃП
ЂЦШєвввђЙЄзїашвЊЃЌЫћЕФећРэЪБМфВЛГЌЙ§30ЗжжгЃЌдђМзжСЩйећРэЖрЩйЗжжгВХФмЭъЙЄЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪагУ3 000дЊЙКНјФГжжИЩЙћЯњЪлЃЌгЩгкЯњЪлзДПіСМКУЃЌГЌЪагжЕїВІ9 000дЊЙКНјИУжжИЩЙћЃЌЕЋетДЮЕФНјМлБШЕквЛДЮЕФНјМлЬсИпСЫ20%ЃЌЙКНјИЩЙћЪ§СПБШЕквЛДЮЕФ2БЖЛЙЖр300 kg.ШчЙћГЌЪаАД9дЊ/kgЕФМлИёГіЪлЃЌЕБДѓВПЗжИЩЙћЪлГіКѓЃЌгрЯТЕФ600 kgАДЪлМлЕФАЫелЪлЭъЃЎ
(1)ИУжжИЩЙћЕквЛДЮЕФНјМлЪЧЖрЩйЃП
(2)ГЌЪаЯњЪлетжжИЩЙћЙВгЏРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() жСЕу
жСЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
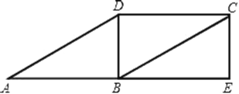
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧОиаЮЃЛ
ЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧыФужБНгаДГі
ЃЌЧыФужБНгаДГі![]() ЕФжЕЃЈВЛвЊЧѓаДЙ§ГЬЃЉ
ЕФжЕЃЈВЛвЊЧѓаДЙ§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌжБЯпyЃНЉ![]() x+2
x+2![]() гыxжсЃЌyжсЗжБ№НЛгкAЃЌBСНЕуЃЌвдAЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуBЃЌЕуPЪЧХзЮяЯпЩЯвЛЕуЃЌСЌНгOPЃЌAPЃЎ
гыxжсЃЌyжсЗжБ№НЛгкAЃЌBСНЕуЃЌвдAЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуBЃЌЕуPЪЧХзЮяЯпЩЯвЛЕуЃЌСЌНгOPЃЌAPЃЎ
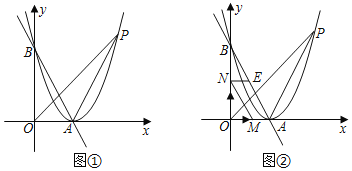
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЁїAOPЕФУцЛ§ЪЧ3![]() ЃЌЧѓPЕузјБъЃЛ
ЃЌЧѓPЕузјБъЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЖЏЕуMЃЌNЭЌЪБДгЕуOГіЗЂЃЌЕуMвд1ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШбиxжсе§АыжсЗНЯђдШЫйдЫЖЏЃЌЕуNвд![]() ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШбиyжсе§АыжсЗНЯђдШЫйдЫЖЏЃЌЕБЦфжавЛИіЖЏЕуЭЃжЙдЫЖЏЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЌЙ§ЕуNзїNEЁЮxжсНЛжБЯпABгкЕуEЃЎШєЩшдЫЖЏЪБМфЮЊtУыЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЫФБпаЮAMNEЪЧСтаЮЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШбиyжсе§АыжсЗНЯђдШЫйдЫЖЏЃЌЕБЦфжавЛИіЖЏЕуЭЃжЙдЫЖЏЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЌЙ§ЕуNзїNEЁЮxжсНЛжБЯпABгкЕуEЃЎШєЩшдЫЖЏЪБМфЮЊtУыЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЫФБпаЮAMNEЪЧСтаЮЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
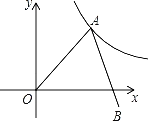
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯгавЛЕуAЃЌСЌНсOAЃЌНЋЯпЖЮAOШЦЕуAФцЪБеыа§зЊ60ЁуЕУЕНЯпЖЮABЃЎШєЕуAЕФКсзјБъЮЊtЃЌЕуBЕФзнзјБъЮЊsЃЌдђsЙигкtЕФКЏЪ§НтЮіЪНЮЊ_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯгавЛЕуAЃЌСЌНсOAЃЌНЋЯпЖЮAOШЦЕуAФцЪБеыа§зЊ60ЁуЕУЕНЯпЖЮABЃЎШєЕуAЕФКсзјБъЮЊtЃЌЕуBЕФзнзјБъЮЊsЃЌдђsЙигкtЕФКЏЪ§НтЮіЪНЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com