
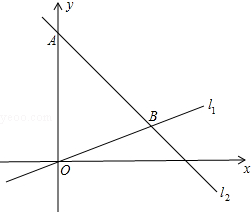
 ��֪����ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��24��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��18��6����
��֪����ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��24��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��18��6�������� ��1����ͼ�п��Կ���l1��������������l2��һ�κ��������ݵ�A��B�����꣬�ô���ϵ�����������l1��l2�Ľ���ʽ��
��2����֪��C�������꼰��C��ֱ��l1�ϣ���õ�C�ĺ����ꣻ����֪���˵�D�ĺ����꣬��D��ֱ��l2�ϣ��õ�D�����ꣻ���ݾ��ε����=��������������þ���CDEF�����ꣻ
��3�����������CDEF�����ΪS��Ȼ���ú���a�Ĵ���ʽ��ʾ���S���õ�һ�����κ��������ݶ��κ��������ֵ��������þ���CDEF����������
��� �⣺��1����ֱ��l1�ı���ʽΪy=k1x��
�߹���B��18��6����
��18k1=6��
��ã�k1=$\frac{1}{3}$��
��ֱ��l1�ı���ʽΪy=$\frac{1}{3}$x��
��ֱ��l2�ı���ʽΪy=k2x+b��
�߹���A ��0��24����B��18��6��
��$\left\{\begin{array}{l}{b=24}\\{18{k}_{2}+b=6}\end{array}\right.$����ã�k2=-1��b=24��
��ֱ��l2�ı���ʽy=-x+24��
��2���١ߵ�C��ֱ��l1�ϣ�
�ҵ�C��������Ϊa��
��a=x��
��ã�x=3a��
���C��������3a��a����
��CD��y�ᣬ
���D�ĺ�����Ϊ3a��
�ߵ�D��ֱ��l2�ϣ�
��y=-3a+24��
��D��3a��-3a+24����
�ڡ�C��3a��a����D��3a��-3a+24��
��CF=3a��CD=-3a+24-a=-4a+24��
�߾���CDEF�����Ϊ60��
��S����CDEF=CF•CD=3a����-4a+24��=60��
���a=1��a=5��
��a=1ʱ��3a=3����C��3��1����
��a=5ʱ��3a=15����C��15��5����
������������C����������3��1����C��15��5����
��3������ε����ΪS����S=CF•CD=3a��-4a+24��=-12a2+72a=-12��a2-6a+32-9��=-12��a-3��2+108��
�ߣ�a-3��2��2���൱a=3ʱ��S�����ֵ108��
���� ������Ҫ�������ϵ���������ε���������κ�����ֵ��һ�κ������ۺ�Ӧ�ã��������մ���ϵ�����ǽ���ڣ�1��С��Ĺؼ������ݵ�C�������꼰����ֱ�ߵĽ���ʽ��õ�C����D�������ǽ���ڣ�2��С��Ĺؼ����ڵڣ�3��С���У����������ֵ���뵽���κ����ǽ����һ��˼·��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
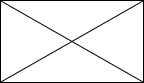 ��ͼ������ABCD�������Խ��߷ֳ��ĸ�С�����Σ�����ĸ�С�����ε��ܳ��ĺ���80cm���Խ��߳���12cm����ô���ε��ܳ��Ƕ��٣�
��ͼ������ABCD�������Խ��߷ֳ��ĸ�С�����Σ�����ĸ�С�����ε��ܳ��ĺ���80cm���Խ��߳���12cm����ô���ε��ܳ��Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
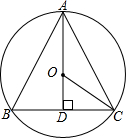 ��֪��������ABC�����Ϊ9$\sqrt{3}$cm��������������εı߳������ľࡢ�뾶���ܳ���
��֪��������ABC�����Ϊ9$\sqrt{3}$cm��������������εı߳������ľࡢ�뾶���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
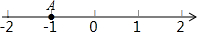 ��ͼ�������ϵĵ�A����ʾ�����ǣ�������
��ͼ�������ϵĵ�A����ʾ�����ǣ�������| A�� | -1 | B�� | -0.5 | C�� | 0 | D�� | -1��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com