
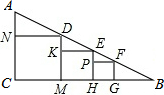
 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.分析 (1)由条件可证明△DKE∽△EPF,再结合正方形的性质,可分别表示出DK、PE,代入可求得PF,可得到答案;
(2)由已知条件DN=10=10×($\frac{4}{5}$)0,KE=8=10×($\frac{4}{5}$)1,PF=$\frac{32}{5}$=10×($\frac{4}{5}$)2,找到规律第n个正方形的边长=10×($\frac{4}{5}$)n-1,从而求解.
解答 解:∵四边形NCMD、四边形KMHE均为正方形,
∴∠DKE=∠DKE,KE∥PF,
∴∠DEK=∠EFP,
∴△DKE∽△EPF,
∴$\frac{DK}{PE}$=$\frac{KE}{PF}$,
又∵DK=10-8=2,KE=8,PE=8-PF,
∴$\frac{2}{8-PF}$=$\frac{8}{PF}$,
解得PF=$\frac{32}{5}$,
即正方形HGFP的边长为$\frac{32}{5}$;
(2)∵DN=10=10×($\frac{4}{5}$)0,
KE=8=10×($\frac{4}{5}$)1,
PF=$\frac{32}{5}$=10×($\frac{4}{5}$)2,
∴第四个正方形的边长=10×($\frac{4}{5}$)3=$\frac{128}{25}$,
∴第n个正方形的边长=10×($\frac{4}{5}$)n-1,
∴从第三个正方形起,第p个正方形的边长=10×($\frac{4}{5}$)p+2.
点评 本题考查了正方形的性质,相似三角形的判定与性质,解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系.


科目:初中数学 来源: 题型:选择题
 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )| A. | L≤40.2 | B. | L≥39.98 | C. | 39.98≤L≤40.02 | D. | 39.8≤L≤40.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
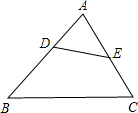 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
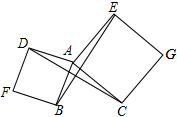 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
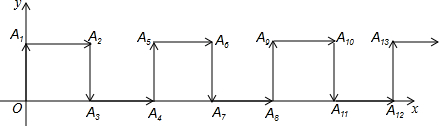
| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com