
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地. 
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 , 为什么?
【答案】
(1)解:设所围矩形ABCD的长AB为x米,则宽AD为 ![]() (80﹣x)米
(80﹣x)米
依题意,得x ![]() (80﹣x)=750
(80﹣x)=750
即,x2﹣80x+1500=0,
解此方程,得x1=30,x2=50
∵墙的长度不超过45m,∴x2=50不合题意,应舍去
当x=30时, ![]() (80﹣x)=
(80﹣x)= ![]() ×(80﹣30)=25,
×(80﹣30)=25,
所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2
(2)解:不能.
因为由x ![]() (80﹣x)=810得x2﹣80x+1620=0
(80﹣x)=810得x2﹣80x+1620=0
又∵b2﹣4ac=(﹣80)2﹣4×1×1620=﹣80<0,
∴上述方程没有实数根
因此,不能使所围矩形场地的面积为810m2
【解析】(1)设所围矩形ABCD的长AB为x米,则宽AD为 ![]() (80﹣x)米,根据矩形面积的计算方法列出方程求解.(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.
(80﹣x)米,根据矩形面积的计算方法列出方程求解.(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
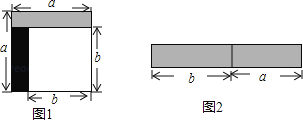
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下题:
计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某校有一长方形操场,长为x m,宽为y m,为了美化校园环境,学校决定在操场四周修建m m宽的绿化带,负责后勤的王老师让八年级某班学生计算一下剩下操场的面积,可是该班学生计算出了两种结果:一种是(xy-2mx-2my)m2,另一种是(xy-2mx-2my+4m2)m2,并且为此争论不休,作为一名八年级学生,你能运用所学的知识来帮助他们判断对错吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点. 
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
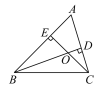
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com