
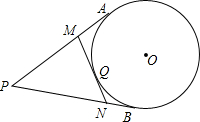
 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8. 科目:初中数学 来源: 题型:选择题
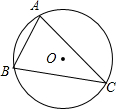 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
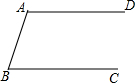 如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).
如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
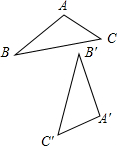 已知△A′B′C′是由△ABC经过顺时针旋转而得.
已知△A′B′C′是由△ABC经过顺时针旋转而得.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
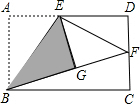 如图,在长方形ABCD中,AB=3,BC=2$\sqrt{6}$,点E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.
如图,在长方形ABCD中,AB=3,BC=2$\sqrt{6}$,点E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
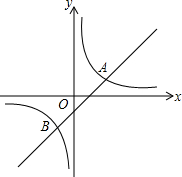 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
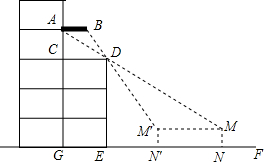 周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)
周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com