
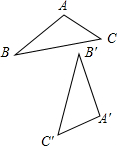
 已知△A′B′C′是由△ABC经过顺时针旋转而得.
已知△A′B′C′是由△ABC经过顺时针旋转而得.分析 (1)根据对应点的连线段的垂直平分线的交点就是对称中心即可找到对称中心.
(2)由△AOC≌△A′OC′得∠ACO=∠OC′P所以A、O、C′、P四点共圆,所以∠P+∠COC′=180°由此可以求出∠P.
解答  解:(1)如图,连接BB′,AA′,线段BB′、AA′的垂直平分线的交点O就是对称中心.
解:(1)如图,连接BB′,AA′,线段BB′、AA′的垂直平分线的交点O就是对称中心.
(2)连接OA、OC、OA′、OB′
∵∠AOA′=∠COC′,
∴∠AOC=∠A′OC′,
在△AOC和△A′OC′中,
$\left\{\begin{array}{l}{OA=OA′}\\{∠AOC=∠A′OC′}\\{OC=OC′}\end{array}\right.$,
∴△AOC≌△A′OC′,
∴∠ACO=∠OC′P,
∴A、O、C′、P四点共圆,
∴∠P+∠COC′=180°,
∵∠COC′=120°,
∴∠P=60°.
补充:由∠ACO=∠OC′P,
∴∠ACO+∠PCO=180°,
∴∠OC′P+∠OCP=180°,
∴∠P+∠COC′=180°,
以下相同.
点评 本题考查旋转的有关概念,记住旋转中心是对应点连线段的垂直平分线的交点,第二个问题有难度,需要通过四点共圆去解决.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
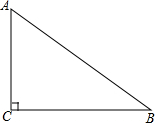 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相切或相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
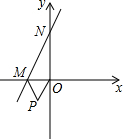 如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
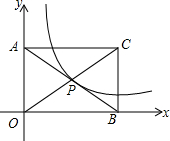 如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
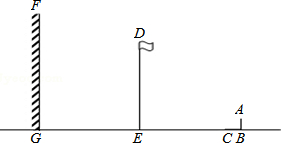
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
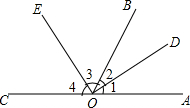 ∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.
∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com