
【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 30 | 45 |
租金(元/辆) | 450 | 600 |
已知某中学计划租用![]() 两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆B型号客车?
(2)若七年级师生共有380人,请写出所有可能的租车方案.
【答案】(1)最多能租用7辆![]() 型号客车;(2)有两种租车方案,方案一:租
型号客车;(2)有两种租车方案,方案一:租![]() 型号客车4辆、
型号客车4辆、![]() 型号客车6辆;方案二:租
型号客车6辆;方案二:租![]() 型号客车3辆、
型号客车3辆、![]() 型号客车7辆.
型号客车7辆.
【解析】
(1)设租用B型号客车x辆,则租用A型号客车(10-x)辆,根据总租金=600×租用B型号客车的辆数+450×租用A型号客车的辆数结合租车的总费用不超过5600元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再取其中的最大整数值即可得出结论;
(2)设租用B型号客车x辆,则租用A型号客车(10-x)辆,根据座位数=45×租用B型号客车的辆数+30×租用A型号客车的辆数结合师生共有380人,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再结合(1)的结论及x为整数,即可得出各租车方案.
(1)设租用![]() 型号客车
型号客车![]() 辆,则租用
辆,则租用![]() 型号客车
型号客车![]() 辆,
辆,
依题意,得:![]() ,
,
解得:![]()
又∵![]() 为整数,
为整数,
∴![]() 的最大值为7.
的最大值为7.
答:最多能租用7辆![]() 型号客车.
型号客车.
(2)设租用![]() 型号客车
型号客车![]() 辆,则租用
辆,则租用![]() 型号客车
型号客车![]() 辆,
辆,
依题意,得:![]() ,
,
解得:![]()
又∵![]() 为整数,且
为整数,且![]() ,
,
∴![]() .
.
∴有两种租车方案,方案一:租![]() 型号客车4辆、
型号客车4辆、![]() 型号客车6辆;方案二:租
型号客车6辆;方案二:租![]() 型号客车3辆、
型号客车3辆、![]() 型号客车7辆.
型号客车7辆.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,已知∠MAN=120°,AC平分∠MAN,∠ABC=∠ADC=90°,则能得到如下两个结论:①DC=BC;②AD+AB=AC. 请你证明结论②.
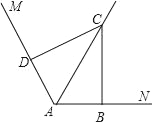
(2)如图,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
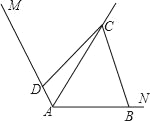
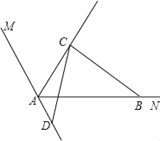
(3)如图3,如果D在AM的反向延长线上,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC=∠ADC,其他条件不变,(1)中的结论是否仍然成立?若成立,请直接回答;若不成立,你又能得出什么结论,直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
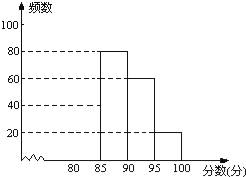
【题目】某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
分数段 | 频数 | 频率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
根据以上图表提供的信息,解答下列问题:
(1)写出表中x,y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论(只要写出一条结论).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 互补.
互补.
(1)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)如图![]() ,
,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() ;
;
(3)如图![]() ,在(2)的条件下,连接
,在(2)的条件下,连接![]() ,
,![]() 是
是![]() 上一点使
上一点使![]() ,作
,作![]() 平分
平分![]() ,问
,问![]() 的大小是否发生变化?若不变,请求出求值;若变化,说明理由.
的大小是否发生变化?若不变,请求出求值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.张涛在政府的扶持下销售一种进价为每件20元的新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
若只在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润=销售额-成本-广告费). 若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本(含进价)为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为W外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为W外(元)(利润=销售额-成本-附加费).
(1)求y与x的函数关系式(不必写x的取值范围);
(2)分别求出W内,W外与x间的函数关系式(不必写x的取值范围);
(3)在国内销售时,每月的销售量在什么范围内,张涛才不会亏本?
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com